Évaluation des compétences
Un élève, incapable de grimper sur un arbre, souhaite mesurer sa hauteur. Il mesure que l’ombre de l’arbre est de 10 m pendant la recréation. Au même moment, le mât du drapeau vertical de 10 m projette une ombre de 2,5 m.
Aide cet élève à calculer la hauteur de cet arbre.

Objectifs pédagogiques
• Comprendre et appliquer le théorème de Thalès dans un triangle rectangle.
• Savoir identifier des segments proportionnels et les utiliser pour résoudre des problèmes géométriques.

Structure du cours
I. Propriété de Thalès dans le triangle ;
II. Utilisation des propriétés de Thalès ;
III. Triangles semblables ;

Introduction

Thalès de Milet (vers 625 av. J.-C. - 547 av. J.-C.) est considéré comme l’un des premiers mathématiciens et philosophes grecs à s'intéresser aux propriétés géométriques. Son travail sur la propriété qui porte son nom découle principalement de son observation méthodique des proportions et des ombres, ainsi que de son intérêt pour les applications pratiques de la géométrie.

I. Propriété de Thalès dans le triangle

A) La propriété directe Thalès dans le triangle

• Énoncé :
« Si deux droites parallèles coupent deux droites sécantes, alors les segments formés sur ces droites sécantes sont proportionnels. »
Autrement dit :

Soit ABC un triangle, \(M\) un point de \((AB)\) et \(M’\) un point de \((AC)\). Si \(\left( {MM'} \right)\parallel (BC)\), alors \(\frac{{AM}}{{AB}} = \frac{{AM'}}{{AC}}\).

• Conditions d’application de la Propriété de Thalès
1. Avoir deux droites parallèles.
2. Ces droites coupent deux droites sécantes.
3. Les longueurs doivent être mesurées sur une même direction.

• Démonstration de la propriété de Thalès

Soit ABC un triangle, M un point de la droite \((AB)\) et M’ un point de \((AC)\) tel que : \(\left( {MM'} \right)\parallel (AB)\)
Démontrons que \(\frac{{AM}}{{AB}} = \frac{{AM'}}{{AC}}\).
En effet,

a) Si \(M \in \left[ {AB} \right)\) et \(M’ \in \left[ {AC} \right)\)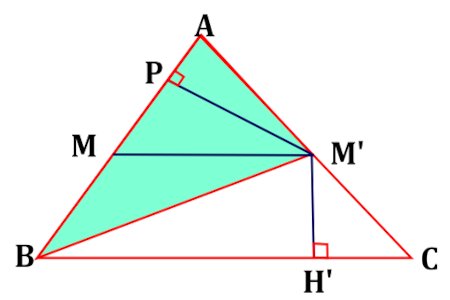
Utilisons différentes expressions de l’aire du triangle ABM’
\(\frac{{AM}}{{AB}} = \) \(\frac{{AM \times \frac{{M'P}}{2}}}{{AB \times \frac{{M'P}}{2}}} = \) \(\frac{{aire\left( {AMM'} \right)}}{{aire\left( {ABM'} \right)}}\)
Utilisons différentes expressions de l’aire du triangle AMC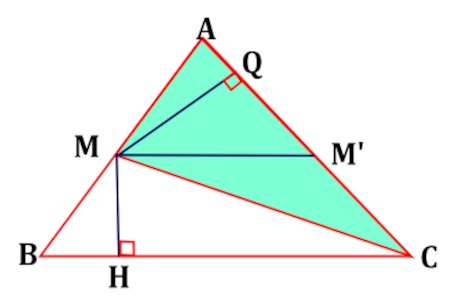
\(\frac{{AM'}}{{AC}} = \) \(\frac{{AM' \times \frac{{MQ}}{2}}}{{AC \times \frac{{MQ}}{2}}} = \) \(\frac{{aire\left( {AMM'} \right)}}{{aire\left( {ACM} \right)}}\).
Il suffit de démontrer que : \({aire\left( {ABM’} \right)}\) \(=\) \({aire\left( {ACM} \right)}\)
Les triangles BMA et BM’C ont le même aire \(A \), car ils ont le coté [BC] commun et de hauteurs égales : \(M'H' = MH\).
L’aire de chacun des triangles ABM’ et ACM est celle du triangle ABC diminuée de \(A \),
Donc, \({aire\left( {ABM’} \right)}\) \(=\) \({aire\left( {ACM} \right)}\) alors \(\frac{{aire\left( {AMM'} \right)}}{{aire\left( {ABM'} \right)}} = \frac{{aire\left( {AMM'} \right)}}{{aire\left( {ACM} \right)}}\) alors \(\frac{{AM}}{{AB}} = \frac{{AM'}}{{AC}}\)

b) Si \(M \notin \left[ {AB} \right)\) et \(M’ \notin \left[ {AC} \right)\)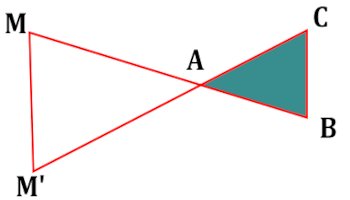
Un utilisera la symétrie de centre A et le résultat précèdent (confère exercice)

B) Réciproque de la propriété de Thales

La réciproque d'une propriété ou d'un théorème est une affirmation obtenue en inversant les hypothèses et la conclusion de cette propriété. En d'autres termes, si une propriété dit :
"Si A, alors B", sa réciproque est : "Si B, alors A".

Énoncé de la réciproque de la propriété de Thales
" ABC est un triangle, M est un point de (AB), M’ un point de (AC) tels que la position de M par rapport à A et B soit la même que celle de M’ par rapport à A et C."
Si \(\frac{{AM}}{{AB}} = \frac{{AM'}}{{AC}}\) alors \(\left( {MM'} \right)\parallel \left( {BC} \right)\)

C) Conséquence de la propriété de Thales

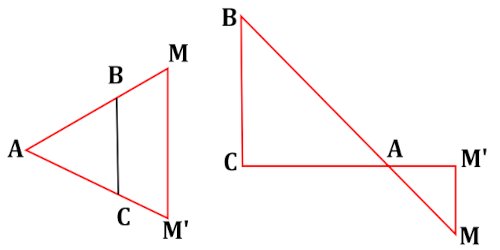Soit un triangle ABC, M un point de \(\left( {AB} \right)\) et M’ un point de \(\left( {AC} \right)\)
Si \(\left( {MM'} \right)\parallel \left( {BC} \right)\) alors \(\frac{{AM}}{{AB}} = \frac{{AM'}}{{AC}} = \frac{{MM'}}{{BC}}\)

II. Utilisation des propriétés de Thalès

a) Construire une quatrième proportionnelle

On donne trois segments de mesure a, b, et c.
On veut construire la quatrième proportionnelle des nombres a, b et c pris dans cet ordre. Cela revient à construire un segment [MN] tel que : \(\frac{a}{b} = \frac{c}{{MN}}\).
Pour cela,
• On trace deux demi-droites de même origine ;
• Sur l’une des demi-droites, on marque A et B tels que : \(MA = a\) et \(MB = b\) ;
• Sur l’autre demi-droite, on marque C tel que : \(MC = c\) ;
• On trace la droite parallèle à \(AC\) qui passe par B : elle coupe \(MC\) ao point N.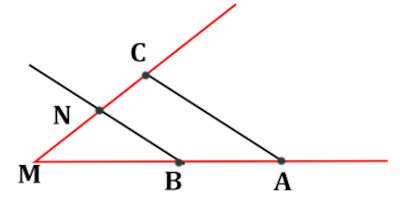
D’après la propriété de Thales dans le triangle MAC : \(\frac{{MA}}{{MB}} = \frac{{MC}}{{MN}} \Rightarrow \frac{a}{b} = \frac{c}{{MN}}\)
Donc MN est la quatrième proportionnelle des nombres a, b et c

b) Le calcule des distances
(Confère exercices)

c) Démonstration du parallélisme des droites
(Confère exercices)

III. Triangles semblables

a) Propriétés des triangles semblables

ABC est un triangle, M est un point de [AB] et M’ le point de [AC] tel que (MM’ soit parallèle à (BC).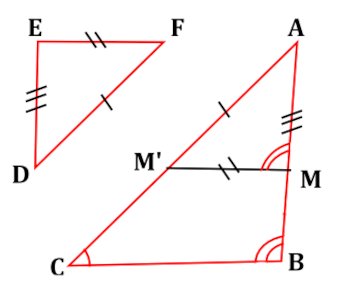
On dit que ABC et AMM’ sont des triangles semblables.
D’après Thales, \(\frac{{AM}}{{AB}} = \frac{{AM'}}{{AC}} = \frac{{MM'}}{{BC}}\) De plus \(mes\widehat {M'} = mes\widehat C\) et \(mes\widehat M = mes\widehat B\)
Les triangles DEF et AMM’ sont superposables. On dit que ABC et DEF sont des triangles semblables, car :
• A et D sont des sommets homologues ;
• \(\widehat A\) et \(\widehat D\) sont des angles homologues
• [AB] et [DE] sont des cotes homologues.

Propriétés :
• Si deux triangles sont semblables, alors leurs cotés sont deux à deux proportionnelles.
• Si deux triangles sont semblables, alors leurs angles sont deux à deux de même mesure.
• Si deux triangles ont leurs cotés deux à deux proportionnels, alors ils sont semblables.
• Si deux triangles ont leurs angles deux à deux de même mesure, alors ils sont semblables.