Première
C & E & D & TI
Physique
Correction exercice
Bonjour ! Notre page Facebook, la suivre pour nos prochaines publications
Contenu 1
Exercice I
1- Calcule le diamètre du soleil.
1- Calcule le diamètre du soleil.\(\tan (\theta ) = \frac{{\frac{d}{2}}}{{ST}}\)\( = \frac{d}{{2ST}} \simeq \theta \)\( \Rightarrow \alpha = 2\theta \)\( = \frac{d}{{ST}}\)
\(d = 9,3 \times {10^{ - 3}}.150 \times {10^9}\)\( = 1,4 \times {10^6}{\rm{ }}km\)
2– Calcule du temps que met un rayon lumineux émis par le soleil pour parvenir à la terre.
\(c = \frac{{ST}}{t} \Rightarrow \)\(t = \frac{{ST}}{c}\)\( = 500s = 8,33\min \)
3- Calcule de la valeur approchée de la distance terre-lune
\(c = \frac{{TL}}{t}\)\( \Rightarrow TL = c.t\)\( = 3 \times {10^8}.\frac{{2,58}}{2}\)\( = 5,37 \times {10^8}{\rm{ m}}\)
Exercice II
Calcule de la hauteur du poteau.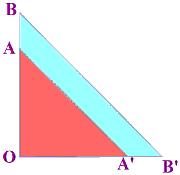
Soit OA la hauteur du palmier, OA’ la longueur de son ombre, OB la hauteur du poteau et OB’ la longueur de son ombre.
Soit OA la hauteur du palmier, OA’ la longueur de son ombre, OB la hauteur du poteau et OB’ la longueur de son ombre.
\(\left\{ \begin{array}{l}OB = 7{\rm{ m}}\\OB' = 3{\rm{ m}}\end{array} \right.\) et \({\rm{ }}\left\{ \begin{array}{l}OA = ?\\OA' = 4{\rm{ m}}\end{array} \right.\)
D’après le théorème de Thales, nous avons:
\(\frac{{OA'}}{{OB'}} = \frac{{OA}}{{OB}}\)\( \Rightarrow OA = OB\frac{{OA'}}{{OB'}}\) \(OA = 7\frac{4}{3} = 9,33{\rm{ m}}\)
Exercice III
t=500s et c=3 108m/s
1 Calcule de la distance TS: \(TS = c.t\)\( = 3 \times {10^8}.500\)\(150 \times {10^6}km\)
La distance parcourue en une année-lumière (A.L). \(d = {3.10^8} \times 365,25 \times 24 \times 3600\)\( = 9,{467.10^{15}}m\)
\(\left\{ \begin{array}{l}1.{\rm{AL}} \to 9,467 \times {10^{25}}m\\TS \to 1,44 \times {10^{11}}m\end{array} \right.\) \(TS = 1,{52.10^{ - 5}}AL\)
Exercice V
Soient tL le temps que met l’éclair (lumière) pour parvenir à l’observateur et cL sa vitesse correspondante.
Soient tS le temps que met le son pour parvenir à l’observateur et cS sa vitesse correspondante.
\({t_L}{\rm{ = }}\frac{{\rm{d}}}{{{{\rm{C}}_{\rm{L}}}}}\) , \({t_s} = \frac{{\rm{d}}}{{{{\rm{C}}_{\rm{S}}}}};{\rm{ }}\)
La durée entre l’éclair et son son correspondant est: \(t = \frac{d}{{{C_S}}} - \frac{d}{{{C_L}}}\)\( = d\left( {\frac{1}{{{C_S}}} - \frac{1}{{{C_L}}}} \right)\)
\(\frac{1}{{{C_L}}} \simeq 0{\rm{ }}\) d’où \(t \simeq \frac{d}{{{C_S}}}\)
\(d\left( m \right) \simeq {C_S}t\) \(d\left( {Km} \right) = {331.10^{ - 3}}t\) \( = 0,33t\) \({\rm{or }}\) \(0,33{\rm{ }} = {\rm{ }}\frac{1}{3}\)
\(d(Km) = \frac{t}{3}\)
