Objectifs pédagogiques :
• Identifier les éléments d’un algorithme ;
• Identifier les structures de contrôle ;
• Construire un organigramme ;
• Exécuter un algorithme ayant une structure alternative ;
• Exécuter un algorithme simple ;
• Exécuter des algorithmes itératifs.
Situation problème :
Ali est né et vit à Maroua depuis pratiquement 17 ans, après son baccalauréat, il décide faire le concours de L’ENAM, pour cela, il doit se rendre impérativement à Yaoundé où il n’y a jamais été auparavant. Disposant d’un téléphone Android doté d’un assistant de navigation GPS :
1) Quelles sont les données qu’il doit entrer pour obtenir l’itinéraire qui mène à l’ENAM ?
2) Quel est alors le résultat obtenu ?
I. Notion d’algorithme
a) Définitions
L’algorithme décrit formellement ce que doit faire l’ordinateur pour arriver à un but bien précis. Ce sont les instructions qu’on doit lui donner. Ces instructions sont souvent décrites dans un langage clair et compréhensible par l’être humain : faire ceci, faire cela si le résultat a telle valeur, et ainsi de suite.
Un algorithme est dont une suite finie et ordonnée d’opérations élémentaires donc l’exécution pas à pas permet de résolution un problème ; C’est une séquence d’instructions qui décrit comment résoudre un problème particulier.
L’algorithmique est la science qui étudie les algorithmes.
b) Caractéristiques d’un algorithme
Un programme est la réalisation d’un algorithme dans un langage donné (proche de celle de la machine);
Un algorithme doit respecter un certain nombre de règles : Non ambigüe, compréhensible, ordonné, durable, lisible et fini, Simple.
• Simplicité : la description des procédés doit être d’une longueur finie.
• Le déterminisme : Un algorithme est dit déterministe si les étapes d’exécution sont bien fixées et ne conduisent à des choix aléatoires.
• La terminaison (finitude) : L’algorithme doit produire la sortie souhaitée avec un nombre fini d’étapes.
• La généralité : L’algorithme s’applique à tous les problèmes d’une même classe.
• La correction d’un algorithme signifie qu’il doit répondre au problème pour lequel il a été conçu.
• La clarté (lisibilité) d’un algorithme implique que le concepteur s’assure qu’il est facile à comprendre et à interpréter. Chaque opération doit être définie d’une manière précise.
• La documentation d’un algorithme consiste à l’insertion des connecteurs qui facilite la compréhension du programme.
Un algorithme est dit efficace lorsque les opérations sont suffisamment simples et qu’elle s’exécute le plus rapidement possible.
c) Structure générale d’un algorithme
Tout comme le corps humain, un algorithme a trois parties :
c.1) L’entête
Il permet tout simplement d’identifier l’algorithme.
La syntaxe est la suivante : algorithme nom de l’algorithme ;
Exemple d’entête : algorithme Aire_cercle
c.2) La partie déclarative
Ele permet de déclarer tous les objets à utiliser dans le corps de l’algorithme tels que : variable, constante, structure, fonction, procédure. Variables et constantes
Une constante est une quantité ayant une valeur fixe tout au long d’un algorithme. En d’autres termes sa valeur ne change pas.
Elle est caractérisée par deux éléments : son nom (identificateur) et sa valeur.
Une variable est une quantité pouvant prendre différentes valeurs tout au long d’un algorithme. Elle est caractérisée par trois éléments :
• Son identificateur (nom) ;
• Son type et ;
• Son contenu.
Il existe 5 types de variable existent :
• Entier (integer),
• Réel (real),
• Booléen (boolean),
• Caractère (character),
• Chaîne de caractère (string).
c.3) Le corps de l’algorithme
Compris entre les mots « début » et « fin » contient les instructions, les délimiteurs, les opérations de traitements et les commentaires.
1. Instructions
Les instructions sont les ordres de traitement respectant les actions simples dans l’exécution d’un algorithme.
Il existe plusieurs instructions :
– L’instruction d’affectation : Elle consiste à attribuer une valeur à une variable. On utilise le symbole « ← » qui signifie égal « = » en mathématiques.
Exemple : a ← 2 signifie que « a » prend la valeur 2 ou 2 est affecté à « a » ou a = 2.
– L’instruction de sortie : Elle consiste à écrire une donnée sur un périphérique de sortie tel que l’écran ou l’imprimante…
Elle se réduit aux verbes : afficher (); écrire ().
Sa syntaxe est : affiche (“entrer la valeur de a“).
– L’instruction d’entrée : Une entrée consiste à introduire une donnée à partir des sources d’entrée (clavier, souris, crayon optique, …). Elle permet d’affecter à un objet en mémoire une valeur de même type que l’objet.
Elle s’utilise par les mots : lire (), saisir (), affiche ()...
Syntaxe : Saisir (a).
- Les instructions d’incrémentation/ de décrémentation : Elles se rencontrent dans les boucles. L’incrémentation peut être assimilé à un compteur qui à chaque cycle augmente d’une unité (1) ; La décrémentation est la diminution d’une unité à chaque cycle. Pour ce faire on utilise les variables du compteur (i ou j).
Syntaxe: i ← i+1; j ← j-1
2. Les opérateurs
On distingue plusieurs types d’opérateurs :
Les opérateurs arithmétiques :
- Les opérateurs unaires ou monodiques (appliqué à un seul opérande) : -27 ; +10
- Les opérateurs binaires ou diadique (lient deux opérandes) : 12+5 ;
- Les opérateurs logiques ou booléens : ET, OU, NON.
- Les opérateurs relationnels :
• Inférieur (<, <=) ;
• Supérieur (>, >=) ;
• Égalité (=) ;
• Différence (<>).
Activité : algorithme permettant de faire des omelettes.
Algorithme : faire_omelette ()
Objets : Œuf, huile, oignon, tomate, cube, sel, poêle, bol,
Début
Découper les oignons dans le bol ;
Découper la tomate dans le bol ;
Casser les œufs dans le bol ;
Battre les œufs, a tomate et les oignons ;
Mettre l’huile dans la poêle ;
Déposer la poêle au feu pendant 2minutes ;
Mettre le mélange dans l’huile ;
Enlever après 3 minutes ;
Fin
II. Les structures de contrôles
Une structure de contrôle est une structure qui permet d’exécuter un bloc d’instructions lorsqu’un ensemble de conditions est réalisé.
Un bloc d’instructions est un ensemble d’instructions qui doivent être exécutées ensemble.
On distingue 3 structures algorithmiques de base :
• Structure algorithmique linéaire ou séquentielle ;
• Structure algorithmique conditionnelle ;
• Structure algorithmique itérative ou boucle.
II.1 Les structures algorithmiques linéaires ou séquentielles
Les structures séquentielles se caractérisent par une suite d‘actions à exécuter successivement dans l‘ordre énoncé.
Dans cette structure, les actions se suivent, la fin d’une action déclenche le début d’une autre sans interruption.
Une action se termine par un point-virgule (;).
Une structure séquentielle peut donc se présenter de la manière suivante :
Exécuter : « instruction 1 »
Exécuter : « instruction 2 »
…
…
Exécuter : « instruction n »
Fin
Algorithme somme
– Variable a, b: réel
– s: réel
Début
– Écrire (‘’entrer le premier nombre’’);
– Lire (a);
– Écrire (‘’entrer le deuxième nombre’’);
– Lire (b);
– s ← a+b ;
– Écrire (s);
Fin

II.2 Les structures algorithmiques conditionnelles
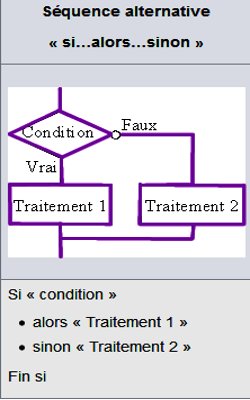
Une structure conditionnelle est dite à forme alternative lorsque le traitement dépend d’une condition à deux états :
• Si la condition est évaluée à vrai, le premier traitement est exécuté ;
• Si la condition est évaluée à faux, le deuxième traitement est exécuté.
L‘instruction si permet de programmer une structure dite de choix (ou alternative), permettant de choisir entre deux instructions ou plus, suivant la valeur d‘une expression jouant le rôle de condition. La seconde partie, introduite par le mot clé SINON, est facultative, de sorte que l‘instruction SI présente deux formes.
On distingue deux types de structures alternatives :
Exercice : racine carré d’un nombre
Algorithme racine_carre
– Var x, y: réel
Début
– Ecrire (‘’enter un nombre’’);
– Lire(x);
– Si x >=0;
y ← sqrt (x);
Ecrire (y);
– Sinon
Ecrire (‘’pas de racine réelle’’);
– Finsi
Fin
II.3 Les structures algorithmiques itératives ou boucles
Une itération ou boucle est une séquence d’instructions destinée à s’exécuter plusieurs fois.
Un cycle est un tour de la boucle.
On distingue deux types d’itérations :
• Itérative complète (pour)
• Itération à condition d’arrêt (tant que, répéter).
II.3.a) Itérative complète (pour)
Dans cette structure, la sortie de la boucle d‘itération s‘effectue lorsque le nombre souhaité de répétition est atteint.
On utilise donc une variable (ou indice) de contrôle d‘itération (i) de la boucle caractérisée par sa valeur initiale, sa valeur finale, son pas de variation.
Sa syntaxe est :
Pour i allant de 0 à 9 Pas de 1 faire
Afficher(i) ;
Fin pour
Exemple calcule de la puissance d’un nombre
Algorithme puissance
Var n, i : entier; x, p: réel
Début
P ← 1;
Pour i ← 1 à n faire
p ← p*x
finPour
Fin
II.3.b) Itérative à condition d’arrêt (tant que, répéter)
1. Itération à condition d’arrêt : La boucle Tant que
• Est une structure dans laquelle la condition est d’abord testée et le traitement exécuté si la condition est remplie.
• S’utilise lorsqu’aucun traitement ne s’exécute avant la condition (le test) et le nombre d’itération n’est pas connu.
• Doit initialiser un compteur (amorçage), incrémenter le compteur à chaque pas (relance), vérifie que le compteur ne dépasse pas la borne supérieurs (test de boucle).
Sa syntaxe est :
Tant que « condition »
• faire « traitement »
Fin tant que
2. Itération à condition d’arrêt (tant que, répéter).
2.1 Itération à condition d’arrêt (tant que).
Lors de l’exécution de l’algorithme, celui-ci arrive sur l’instruction "Tant que". Il évalue l’expression booléenne (condition) Si la condition est vraie, alors le programme exécute les instructions suivantes jusqu’à ce qu’il arrive au "FinTantQue". Une fois ici, il remonte au "Tant Que" et évalue de nouveau l’expression et évalue la condition, si c’est vrai alors il exécute de nouveau les instructions, et ainsi de suite, tant que l’expression retourne vrai.
Si l’expression devient fausse, alors le programme saute à l’instruction située juste après le "FinTantQue".
• Sa syntaxe est : tant que faire (instruction)
Voici un simple exemple qui affiche les chiffres de 1 à 10 :
Algorithme compteur
VAR x : entier
DEBUT
x ← 1
Tant que x<=10 Faire
Afficher x
x ← +1
FinTantQue
FIN
2.2 Itération à condition d’arrêt (répéter).
C’est une structure dans laquelle le traitement est exécuté une fois avant le test et le nombre d’itération n’est pas connu.
• Syntaxe: Répéter (instruction) jusqu’à (condition)
Exemple calcule de la moyenne de plusieurs nombres
Algorithme Moyenne
Var s: réel; note: entier
Début
S ← 0;
i ← 1;
Répéter
Ecrire (‘’donner la note n°:’, i);
Lire (note);
s ← s+note;
i ← i+1;
Jusqu’à i = 10
Ecrire (‘’la moyenne des 10 notes est :’, s/10);
Fin

III. Exécution d’un algorithme
Pour exécuter un algorithme, il suffit de conserver une trace des valeurs en cours des différentes variables et d’exécuter une à une les opérations qui composent l’algorithme (en respectant la sémantique des structures de contrôle) en reportant leur éventuel impact sur les valeurs des différentes variables.
application : Exécuter l’algorithme suivant avec a = -4 et b = -2
(1). Algorithme Plus_grand
(2). Variable a, b, pg : réel ;
(3). Début
(4). Ecrire (’entrer les deux valeurs’) ;
(5). Lire (a, b) ;
(6). Si a>b alors
(7). Pg ← a ;
(8). Sinon
(9). Pg ← b ;
(10). FinSi
(11). Ecrire (‘le plus grand nombre est :’, pg) ;
(12). Fin
| Ligne | Instruc tions | Variables | Valeur de la condition | Ligne sui vante | ||
| a | b | pg | ||||
| 5 | Lire (a,b) | - 4 | - 2 | 9 | ||
| 6 | si a>b | - 4 | - 2 | 7 | ||
| 7 | pg ← a | - 4 | - 2 | Faux | 8 | |
| 8 | sinon | - 4 | - 2 | 9 | ||
| 9 | pg ← b | - 4 | - 2 | - 2 | Vrai | 11 |
| 11 | Ecrire(pg) | - 4 | - 2 | - 2 | Vrai | Fin |
IV. Notion d’organigramme
L’organigramme est une représentation graphique de l’algorithme utilisant des symboles normalisés.
IV.1 Les symboles de l’organigramme
Également connue sous le nom de « symbole d'action », Ce sont les formes qui représentent, un processus, une action ou une fonction. Les symboles les plus largement utilisés dans la création d'organigrammes sont :
Les symboles les plus largement utilisés dans la création d'organigrammes sont :
a) Symboles de traitement
• Symbole général “ traitement ”
Opération ou groupe d'opérations sur des données, instructions, etc.., ou opération pour laquelle il n'existe aucun symbole normalisé.
• Sous-programme
Portion de programme considérée comme une simple opération.
• Entrée - Sortie :
Mise à disposition d'une information à traiter ou enregistrement d'une information traitée.
• Préparation
Opération qui détermine partiellement ou complètement la voie à suivre dans un embranchement ou un sous-programme.
Symbole également utilisé pour préparer une décision ou mettre un aiguillage en position.
b) Symboles logiques
• Embranchement
Exploitation de conditions variables impliquant le choix d'une voie parmi plusieurs.
Symbole couramment utilisé pour représenter une décision ou un aiguillage.
c) Symboles auxiliaires
• Renvoi
Symbole utilisé deux fois pour assurer la continuité lorsqu'une partie de ligne de liaison n'est pas représentée. Il indique que l'étape suivante ou précédente est ailleurs sur l'organigramme.
• Début, fin, interruption
Début, fin ou interruption d'un organigramme, point de contrôle, etc.
• Commentaire
Symbole utilisé pour donner des indications marginales.
IV.2 Sens conventionnel des liaisons
Le sens général des lignes doit être de :
• Haut en bas
• Gauche à droite.
Lorsque le sens ainsi défini n'est pas respecté, des pointes de flèches, à cheval sur la ligne, indiquent le sens utilisé.
Pour inviter un utilisateur à rentrer au clavier une valeur utilisez le mot "Saisir".
Pour simuler l’affichage d’un texte ou d’une valeur sur l’écran, il faut utiliser la pseudo instruction "Afficher" qui prend à sa suite une chaîne de texte ou une variable.
Pour stocker une donnée dans la machine, on utilise le mot "Lire"


