Partie I : Évaluation des ressources / 24 points

Exercice 1 : Vérification des savoirs / 8 points

1. Définition
Générateur électrique : 1 pt
Un générateur électrique est un appareil ou une machine qui convertit une forme d'énergie (telle que l'énergie mécanique, chimique, ou solaire) en énergie électrique.
Les générateurs électriques sont utilisés dans de nombreux contextes pour fournir de l'électricité à des systèmes, des appareils ou des installations. Les exemples courants incluent les générateurs électromécaniques, comme les alternateurs, qui convertissent l'énergie mécanique en énergie électrique, et les piles, qui convertissent l'énergie chimique en énergie électrique.
Lentille mince : 1 pt
Une lentille mince est un élément optique transparent, généralement fait de verre ou de plastique, avec une épaisseur négligeable par rapport à ses distances focales.
Elle est utilisée pour faire converger ou diverger des faisceaux lumineux. Les lentilles minces peuvent être convexes ou concaves, et elles sont couramment utilisées dans des applications telles que les lunettes, les microscopes, les télescopes et les appareils photo. Une lentille mince convergente (ou convexa) fait converger les rayons lumineux vers un point focal, tandis qu'une lentille mince divergente (ou concave) disperse les rayons lumineux.
2. Énoncer la loi de Joule. 1,5pt
La loi de Joule, nommée d’après le physicien anglais James Prescott Joule, est une loi fondamentale en électricité.
Énoncé de la loi de Joule : 1 pt
La quantité de chaleur produite par un courant électrique traversant un conducteur est proportionnelle au carré de l’intensité du courant, à la résistance du conducteur et au temps pendant lequel le courant circule 1pt.
Mathématiquement, elle peut être exprimée comme suit :
\(W = R{I^2}t\)
Où:
• \(W\) est la chaleur produite (en joules),
• \(I\) est l’intensité du courant (en ampères),
• \(R\) est la résistance du conducteur (en ohms),
• \(t\) est le temps pendant lequel le courant circule (en secondes).
3. Énoncé du théorème de l’énergie cinétique
"la variation de l’énergie cinétique d’un système entre deux instants donnés est égale à la somme algébrique des travaux de toutes les forces extérieures agissant sur le système pendant cet intervalle de temps."
\(\Delta {E_C} = \sum {W({F_{ext}})} \)
4) L’énergie cinétique d’un solide en rotation autour d’un axe fixe est donnée par l’expression suivante :
\({E_C} = \frac{1}{2}{J_\Delta }{\omega ^2}\)
5. Répondre par vrai ou faux. 0,5 pt x 3 = 1,5 pt
5.1 Faux. Dans un microscope, la distance focale de l'objectif est généralement plus petite que celle de l'oculaire. L'objectif doit avoir une distance focale courte pour offrir un grand grossissement.
5.2 Faux. Un œil myope voit flou les objets éloignés et net les objets proches. La myopie se caractérise par une mise au point incorrecte des objets éloignés, qui se forme devant la rétine.
5.3 Faux. Un récepteur actif ne transforme pas entièrement l'énergie électrique reçue en énergie utile. Il y a toujours des pertes d'énergie, généralement sous forme de chaleur. Un récepteur qui transformerait entièrement l'énergie en énergie utile serait idéal, mais il n'existe pas en pratique.
6) L'unité du flux magnétique est le Weber, symbolisé par Wb. Un Weber équivaut à un Tesla-mètre carré (T•m²), où un Tesla est l'unité de mesure de l'induction magnétique ou densité de flux magnétique.

Exercice 2 : Application des savoirs / 8 points

1- Interaction lumière-matière / 2 points

On considère un photon de fréquence \(N = 2,4 \times {10^{14}}Hz\)
1.1-Calculons la longueur d’onde de ce photon. 1pt
\(\lambda = \frac{C}{N} = 1,25 \times {10^{ - 6}}\) m
1.2-Calculons l’énergie transportée par ce photon. 1pt
\(E = h \times N \approx \) \(1,6 \times {10^{ - 19}}J\)

2-Circuit électrique/2,5pts

2.1- Faisons le schéma de ce circuit. 1 pt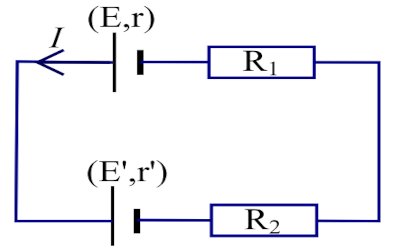
2.2- En appliquant la loi de Pouillet, calculer l’intensité du courant dans le circuit. 1,5pt
\(I = \frac{{E - E'}}{{r + r' + {R_1} + {R_2}}}\)
\(I = \frac{{24 - 8}}{{22}} \approx 0,73A\)
L'intensité du courant dans ce circuit est d'environ 0,73 A (ampères).

3-Quantité de chaleur / 1,5 point

Calculer la quantité de chaleur cédée par 8 kg d’eau pour baisser sa température de 60°C à 25°C.
On donne la chaleur massique de l’eau : 4185J/kg/°C. 2 pts
\(Q = m.C({\theta _f} - {\theta _i}) = \) \( - 1,34 \times {10^6}J\)

4- Énergie mécanique / 2 pts

Calculer son énergie potentielle dans les cas suivants :
a) La référence est au sol. 1 pt
\({E_P} = mg{h_A} = 3,21 \times {10^6}J\)
b) la référence est au sommet B. 1pt
\({E_P} = mg({h_A} - {h_B})\) \( = 1,25 \times {10^6}J\)

EXERCICE 3: Utilisation des savoirs / 8 points

1- Détermination de la distance focale d’une lentille \({L_2}\) /4pts
1.1- Déterminer la position, la nature et la grandeur de l’image \({A_1}{B_1}\) à travers la lentille \({L_1}\).
\( - \frac{1}{{\overline {OA} }} + \frac{1}{{\overline {O{A_1}} }} = \frac{1}{{{f_1}}}\) \( \Rightarrow \overline {O{A_1}} = \frac{{{f_1} \times \overline {OA} }}{{{f_1} + \overline {OA} }}\) \( = 0,75\) m 1pt
Nature : comme ܱ \(\overline {O{A_1}} \succ 0\), l’image est réelle. 0,5pt
Grandeur :
\(\frac{{\overline {O{A_1}} }}{{\overline {OA} }} = \frac{{\overline {{A_1}{B_1}} }}{{\overline {AB} }} \Rightarrow \) \(\overline {{A_1}{B_1}} = \overline {AB} \frac{{\overline {O{A_1}} }}{{\overline {OA} }} = - 1\) cm 0,5pt
1.2 Déterminer la distance focale de la lentille \({L_2}\) et déduire sa nature.
Formule de conjugaison sur \({L_2}\) : \( - \frac{1}{{{O_2}{A_1}}} + \frac{1}{{{O_2}A'}} = \frac{1}{{{f_2}}}\)
\({O_2}{A_1} = {O_1}{O_2} - \) \({O_1}{A_1} = 0,75\) m
Donc \({f_2} = - 0,5\) 1,5pt
La lentille \({L_2}\) est donc divergente. 0,5pt

2-Flux/4pts

2.1-Calculons l’intensité du champ magnétique créé au centre du solénoïde. 2 pts
\(B = 4\pi \times {10^{ - 7}}\frac{{N.I}}{L}\)
\(B = 1,26 \times {10^{ - 3}}T\)
2.2-Calculer le flux magnétique à travers la surface de la bobine. 2pts
\(\Phi = NBS = \pi {R^2}NB\)
\(\Phi = 2,46 \times {10^{ - 3}}Wb\)

Partie B : Évaluation des compétences / 16pts

Situation 1 :
1-Prenons position sur la valeur en eau marquée.
Pour cela, calculons la valeur en eau expérimentale et comparons à la valeur en eau théorique donnée. 1 pt
Eau contenue dans le calorimètre : \({Q_1} = ({m_1} + \mu ){C_e}({\theta _f} - {\theta _1})\)
Eau ajoutée dans le calorimètre : \({Q_2} = {m_2}{C_e}({\theta _f} - {\theta _2})\)
\(\sum\nolimits_i {{Q_i}} = 0\) alors \(\mu = \frac{{{m_2}({\theta _2} - {\theta _f})}}{{({\theta _f} - {\theta _1})}} - {m_1}\)
AN : \(\mu = 18,2g\)
On constate \({\mu _{\exp }} = {\mu _{theo}}\) 1pt
2-Prononçons nous sur la pureté du morceau de fer.
Calculons la chaleur massique expérimentale du fer et comparons à la valeur théorique de 460J/kg/°C. 1pt
Eau contenue dans le calorimètre : \({Q_1} = ({m_e} + \mu ){C_e}({\theta _f} - {\theta _1})\)
Morceau de fer ajouté : \({Q_2} = {m_{fer}}{C_{fer}}({\theta _f} - {\theta _2})\)
D’où \({C_{fer}} = \frac{{\left( {{m_e} + \mu } \right){C_e}\left( {{\theta _1} - {\theta _f}} \right)}}{{{m_{fer}}\left( {{\theta _f} - {\theta _2}} \right)}}\)
\({C_{fer}} = 451,78J/Kg/{}^oC\)
\({C_{fer(\exp )}} \ne {C_{fer(theo)}}\)
On peut donc conclure que le fer utilisé n’est pas pur. 1pt

Situation2
Problème : reconstituer les données qui manquent et comparer aux valeurs trouvées par les deux groupesEn l’absence des frottements, on peut aussi bien utiliser la conservation de l’énergie mécanique ou le théorème de l’énergie cinétique. 1pt
• Calcul de \({h_0}\) : \(\frac{1}{2}mV_1^2 = mg{h_0}\) \( \Rightarrow {h_0} = \frac{{V_1^2}}{{2g}} = 80m\)
• Calcul de \({V_2}\) :
\(\frac{1}{2}mV_1^2 = \frac{1}{2}mV_2^2\) \( + mg{h_2} \Rightarrow {V_2} = \) \(\sqrt {V_1^2 - 2g{h_2}} = 10m/s\) 1,5pt
• Calcule de \({h_3}\) : \(\frac{1}{2}mV_1^2 = \frac{1}{2}mV_3^2 + \) \(mg{h_3} \Rightarrow {h_3} = \frac{{V_1^2 - V_3^2}}{{2g}}\) \( = 60\) m 1,5 pt
C’est le groupe B qui a trouvé les bonnes valeurs. 1,5pt