PARTIE A : Évaluation des ressources (15 points)
Exercice 1 : (5 points)
On considère le polynôme \(P\) défini par : \(P(Z) = {Z^3} - (2 + 3i){Z^2}\) \( - 7Z - 18 + 21i = 0\)
Déterminer les nombres complexes \(a\) et \(b\) tels que : \(P(Z) = (Z - 3i)\) \(({Z^2} + aZ + b)\) 0,75pt
Résoudre dans \(\mathbb{C}\) l’équation \(P(Z) = 0\) 1pt
Le plan complexe est muni d’un repère orthonormé direct \((0;\overrightarrow u ,\overrightarrow v )\). On considère les points \(A\), \(B\) et \(C\) d’affixes respectives \({Z_A} = 3i\), \({Z_B} = - 2 - i\) et \({Z_C} = 4 + i\)
a) Écrire sous forme algébrique \(\frac{{{Z_C} - {Z_A}}}{{{Z_C} - {Z_B}}}\) 0,5pt
b) En déduire la nature exacte du triangle \(ABC\) 0,25pt
a) Déterminer l’écriture complexe de la similitude directe \(S\) du plan de centre \(C\) telle que \(S(B) = A\) 1pt
Déterminer le rapport et l’angle de \(S\). 0,5pt
a) \(Z\) est l’affixe d’un point \(M\) quelconque du plan. En utilisant les points \(A\) et \(B\), donner une interprétation géométrique de \(\left| {\frac{{Z - 3i}}{{Z + 3 + i}}} \right|\) 0,25pt
Déterminer la nature et les éléments caractéristiques de l’ensemble \(\left( \Gamma \right)\) des points M d’affixe Z tels que \(\left|{\frac{{Z - 3i} }{{Z + 3 + i} } }\right| = 2\) 0,75pt
Exercice 2 : (5 points)
1) On considère la fonction \(h\) définie sur \(\mathbb{R}\) par : \(h(x) = \) \(\frac{{3{x^4} + 6{x^2} - 5x + 3}}{{{{({x^2} + 1)}^2}}}\)
a) Vérifier que pour tout \(x \in \mathbb{R}\), \(h(x) = 3 - \frac{{5x}}{{{{({x^2} + 1)}^2}}}\) 0.5pt
b) En déduire une primitive sur \(\mathbb{R}\) de \(h\) et la valeur de l’intégrale \(\int_0^1 {h(x)dx} \) 1,5pt
2) Le tableau ci-dessous représente un réseau routier des différents tronçons possibles d’une ville, ainsi que les routes en km liant les quartiers les uns aux autres. La mairie de la ville souhaite électrifier la ville en utilisant moins de câble possible.
| Tronçons | A - B | A - C | C - B | B - D | B - F | C - E | C - F | E - B | E - D | D - G | E - G | F - G | F- E |
| Distances | 8 | 4 | 5 | 2 | 7 | 3 | 4 | 10 | 1 | 8 | 9 | 6 | 12 |
a) Donner un graphe qui correspond à cette situation. 0.5pt
b) Déterminer la distance minimale entre les quartiers A et G en utilisant l’algorithme de DJIKSTRA. 1.5pt
c) Déterminer le nombre de kilomètres de courant électrique pour électrifier la ville. 1pt
Exercice 3 : (5 points)
Soit \(g\) la fonction définie sur \(\mathbb{R}\) par : \(g(x) = x - 1 + {e^{ - x}}\)
Le tableau de variation de \(g\) est : 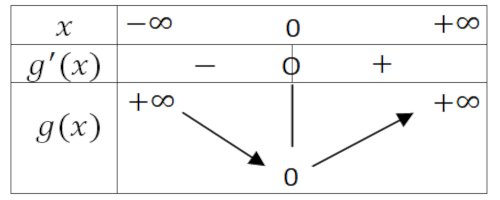 A partir de ce tableau de variation, justifier que \(\forall x \in \mathbb{R}\), \(x + {e^{ - x}} \ge 1\) 0,5pt
A partir de ce tableau de variation, justifier que \(\forall x \in \mathbb{R}\), \(x + {e^{ - x}} \ge 1\) 0,5pt
Soit \(f\) la fonction de \(\mathbb{R}\) vers \(\mathbb{R}\) définie par : \(f(x) = x + \) \(\ln (x + {e^{ - x}})\)
Montrer que l’ensemble de définition de \(f\) est \(Df = \mathbb{R}\). 0,25pt
Calculer la limite de \(f\) en \( + \infty \). 0,25pt
a) Vérifier que \(f(x) = \ln (1 + x{e^{ - x}})\) (\(x\) étant un élément quelconque de \(\mathbb{R}\) 0,25pt
b) En déduire la limite de \( f\) en\( - \infty \). 0,25pt
a) Montrer que pour tout \(x\) de \(\mathbb{R}\), \(f'(x) = \frac{{x + 1}}{{x + {e^{ - x}}}}\) 0,5pt
b) Dresser le tableau de variation de \(f\). 0,75 pt
Tracer la courbe \(\left( {Cf} \right)\) de \(f\) . [On prendra \(\ln (1 - {e^{ - 1}}) = - 0,46\) 0,75pt
\({\left( {{U_n}} \right)_{n \in \mathbb{N}}}\) est la suite numérique définie par : \(\left\{ \begin{array}{l}{U_0} = - 1\\{U_{n + 1}} = f({U_n})\end{array} \right.\) avec \(_{n \in \mathbb{N}}\)
Montrer par récurrence que : \(\forall n \in \mathbb{N}\) , \( - 1 \le {U_n} \le 0\) 0,5pt
Montrer par récurrence que \(\left( {{U_n}} \right)\) est croissante. 0,5pt
En déduire que \(\left( {{U_n}} \right)\) est convergente et calculer sa limite. 0,5pt
PARTIE B : Évaluation des compétences (5 points)
Situation :
Face à la flambé des prix de carburant dans son pays, M. FOUDA a pour projet de lancer dans son usine la fabrication de 4000 véhicules ayant un faible taux de consommation en carburant. Pour ce fait, il décide d’abord de tester un prototype du véhicule avant de lancer la fabrication en série. Il réalise l’expérience suivante : Dans un prototype du véhicule, il introduit du carburant dans le réservoir à débit constant. A l’instant \(t = 0\), le véhicule est mis en marche pour une durée de 10 minutes. Les mesures réalisées permettent de modéliser que le taux \(f(t)\) de consommation de carburant par le véhicule au bout de \(t\) minutes de fonctionnement est solution de l’équation différentielle \(y'' + y' + 0,25y = 0\) et vérifie les conditions
\(f(0)= - 0,2\) et \(f'(0) = 0,2\). Par ailleurs, un véhicule fonctionne normalement lorsque le taux de consommation de carburant au bout de 10 minutes est compris entre 0,005 et 0,006.Afin de faire une estimation sur la somme à prévoir pour la fabrication de tous ces véhicules dans quelques années, le comptable de M. FOUDA constate que la somme \(Z\) en million de FCFA réservée pour cela varie en fonction du temps\(X\) d’années. En posant \(Y = \ln Z\) il a obtenu le tableau statistique suivant :
| X | 1 | 2 | 3 | 4 | 5 |
| Y | 13,3 | 12,9 | 12,5 | 12,1 | 11,7 |
Toutefois, la fabrication d’un véhicule coûte en moyenne 4 millions de FCFA.
Après tous ces tests l’usine fabrique une série de véhicules. On estime que la probabilité qu’un véhicule présente un défaut de fonctionnement à sa sortie de l’usine est égale à 3/10 . On prélève au hasard 20 véhicules sur cette production. On se demande qu’elle est la probabilité d’obtenir au moins deux véhicules présentant un défaut de fonctionnement.
Tâches :
1. Le prototype du véhicule testé par M. FOUDA, fonctionne-t-il normalement ? 1.5pts
2. La somme réservée pour la fabrication des véhicules sera-t-elle suffisante pour fabriquer les 4000 véhicules dans 10 ans? 1.5pts
3. Quelle est la probabilité d’obtenir au moins deux véhicules présentant un défaut de fonctionnement? 1.5pts
Présentation : 0.5pt


