Partie A : Évaluation des ressources : ( 13 points)
Exercice 1 : 5 points
Dans le plan complexe rapporté au repère orthogonal (O;→u,→v)on considère :
I. L’ensemble E des points M(x,y) d’affixe z=reiθ , vérifiant la relation : r2(−cos2θ+1)=9, ( r et θ étant respectivement le module et l’argument de z ). Soient zA=ρeiπ6 et zB=3eiα, (0≤α≤π2 ) les affixes respectifs des points A et B du plan.
Déterminer le module ρ et l’argument α, pour que les points A et B appartiennent à (E). 2pts
II. Les point E, f, C et D d’affixes respectives zE=−12, zF=−12+√32i, zC=1+i√3 et zD=3 .
a) Montrer que le triangle FED est rectangle en E . 1pt
b) Déterminer l’écriture complexe de la similitude plane directe S qui transforme E en F et F en C . 1pt
c) Déterminer les éléments caractéristiques de la similitude S . 1 pt
Exercice 2 : (3 pts)
Un fournisseur d’une compagnie en appareils ménagers est approvisionné par trois marques, notées respectivement M1, M2 et M3. La moitié des appareils de son stock provient de M1, un huitième de M2 , et trois huitièmes de M3 . Ce fournisseur sait que dans son stock, 12% des appareils de la marque M1 sont rouge, que 4 % des appareils de la marque M2 sont rouges et que 10% des appareils de la marque M3 le sont aussi.
On choisit au hasard un appareil emballé dans le stock de ce fournisseur : (on donnera les résultats sous forme de fractions irréductible)
a) Quelle est la probabilité qu'il vienne de M1 ou de M3 ? 1pt
b) Quelle est la probabilité qu'il soit rouge sachant qu'il vienne de M2 ? 1pt
c) Quelle est la probabilité que l'appareil choisi ne soit pas de couleur rouge ? 1pt
Exercice 3 : 5 points
Le plan est muni du repère orthonormé (O ; I, J) (unité graphique : ).
1) On considère la fonction numérique f définie par : f(x)=(ax2+bx+c)ex . La représentation graphique (C) de f passe par les points B(−2;6e−2), C(2;−2e−2) et admet au point d’abscisse x0=1 une tangente (T) perpendiculaire à la droite (D) d’équation y=13(e−1x+2).
a) Montrer que f′(x)=[ax2+(2a +b)x+b+c]ex, f′ étant la fonction dérivée de f. 0.5pt
b) Déterminer en fonction de a, b et c, les expressions de f(−2), f(2) et f′(1) 0.75 pt
c) En déduire de tout ce qui précède que : a=1, b=−2 et c=−2 0,75 pt
2) Soit g la fonction numérique définie sur R parg(x)=23f(x).
a) Étudier les variations de g sur R et dresser son tableau de variation. 1,25pt
b) Tracer dans le repère (O;IJ) la courbe représentative (C′) de la fonction g . 1pt
3) On pose F(x)=(x2−4x+2)ex
a) Vérifier que F′(x)=f(x) pour a=1, b=−2 et c=−2 0,25 pt
b) Déterminer l’aire du domaine D délimitée par la courbe (C′) la droite d’équation x=2 et les axes de coordonnées. 0,5pt
Partie B Évaluation des compétences : 7 points
Monsieur Koul est un fermier qui fait dans l’élevage des poules. Il a relevé dans le tableau suivant le nombre de poules élevé en milliers dans sa ferme :
| Année | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
| Rang de l’année (xi ) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Nombre de poules élevées (yi) | 266 | 281 | a | 281 | 334 | b | 395 |
Les nombres de poules élevées en 2019 et en 2022 ont été effacés par mégarde.
Ces valeurs avaient permis par la méthode des moindres carrées d’obtenir une équation T:y=22x+243 comme équation de la droite de régression de y en x qui permettait à monsieur Koupit d’avoir une estimation du nombre de poules élevées. Monsieur Koul à urgemment besoin de ces valeurs car il voudrait envoyer ses statistiques au Ministère de l’élevage.
M Koul doit se rendre à partir de son domicile, représenté par le sommet A au ministère de l’élevage (sommet G) à fin de déposer ses statistiques. il peut passer par les point de ventes de ses produits représentés par les sommets B, C, D, E, F et H en minimisant le coût. Le réseau routier qui relie ces quartiers est matérialisé sur la figure ci-dessous où les nombres désignent les distances en hm entre 2 quartiers. 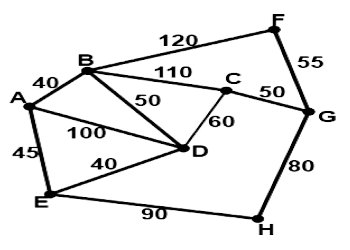 Par ailleurs pour sécuriser sa ferme, Monsieur Koul décide de l’entourer par deux rangées de fils de fer barbelées dont le mètre carré coûte 245FCFA . Son architecte lui indique que le nombre de mètre de fils de fer à acheter est T(2) arrondi à l’unité où T est la solution de l’équation différentielle (E):y″−2y′−3y =(5x+9)e−2x qui admet comme solution particulière P(x)=(x+3)e−2x et dont les conditions initiales de l’équation y″−2y′−3y=0 sont y″(0)=1 et y′(0)=3 . Il dispose d’une somme de 190 000 frs pour l’achat du matériel. On prendra e=2,7 .
Par ailleurs pour sécuriser sa ferme, Monsieur Koul décide de l’entourer par deux rangées de fils de fer barbelées dont le mètre carré coûte 245FCFA . Son architecte lui indique que le nombre de mètre de fils de fer à acheter est T(2) arrondi à l’unité où T est la solution de l’équation différentielle (E):y″−2y′−3y =(5x+9)e−2x qui admet comme solution particulière P(x)=(x+3)e−2x et dont les conditions initiales de l’équation y″−2y′−3y=0 sont y″(0)=1 et y′(0)=3 . Il dispose d’une somme de 190 000 frs pour l’achat du matériel. On prendra e=2,7 .
Tâches :
1- Aider Monsieur Koul à retrouver les valeurs a et b manquantes de son tableau. 2,25pts
2- Quel est le plus court chemin que M Koul devra prendre pour se rendre au ministère ? 2,25pts
3- M Koul pourra-t-il réussir à sécuriser sa ferme ? 2,25pts
Présentation : 0,25pt

