La présentation et le soin apporté à la rédaction seront pris en compte dans l’évaluation de la copie.
Partie A : Évaluation des ressources / 24 points
EXERCICE 1 : Vérification des savoirs 8 points
1. On s'intéresse à un alternateur industriel (type utilisé dans les centrales hydroélectriques et thermiques) et on considère le schéma simplifié ci-dessous : 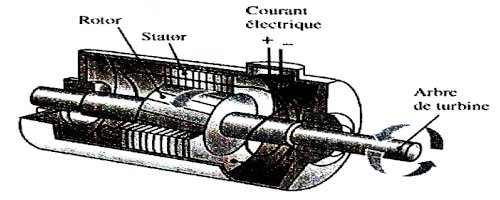 1.1 Quel type de conversion d'énergie l'alternateur permet-il de réaliser (De quelle forme d'énergie vers quelle forme) ? 0,5 pt
1.1 Quel type de conversion d'énergie l'alternateur permet-il de réaliser (De quelle forme d'énergie vers quelle forme) ? 0,5 pt
1.2 Quel est le rôle d’un alternateur ? 0,5 pt
1.3 Qu'est ce qui fait tourner l'arbre de turbine (voir le schéma) dans le cas d'une centrale hydraulique ? Répondre à la même question dans le cas d'une centrale thermique à flammes. ? ??
2 Donner l’expression mathématique traduisant le théorème de l’énergie cinétique dans le cas d’un solide en mouvement de rotation 1 pt
3 Définir : Générateur électrique ; Lentille mince 1 pt
4 Énoncer la règle du l’observateur d’ampère pour déterminer le sens du champ magnétique 1 pt
5 Donner les unités des grandeurs ci-dessous 1pt
5.2 Flux magnétique
5.3 Inductance
6 Énoncer les lois suivantes : 2 pt
6.2 Lois Lenz
6.3 Lois de joule
EXERCICE 2 : Application directe des savoirs et des savoir-faire (8 points)
2-1. On mesure les capacités de deux condensateurs \({C_1} = (20 \pm 1)\mu F\) et \({C_2} = (2,0 \pm 0,1)\mu F\) en parallèles. La capacité équivalente est \(C = {C_1} + {C_2}\).
Déterminer l’incertitude absolue \(\Delta C\) sur la capacité équivalente et donner le résultat sous la forme \(C = {C_0} + \Delta C\). 1,5 pt
2-2. La différence de potentiel aux bornes d’un générateur de f.é.m. E et de résistance interne r = 0,5 Ω est \(U = 12 V\) lorsque celui-ci est parcouru par un courant \(I = 2 A\).
Déterminer la f.é.m. de ce générateur. 1 pt
2-3. Déterminer l’énergie en joules puis en électron volts (eV) d’un photon issu d’un faisceau laser de longueur d’onde \(\lambda = 650nm\). 1,5 pt
Données : \(c = 3 \times {10^8}m/s\), \(h = 6,63 \times {10^{ - 34}}J.s\), \(1eV = 1,6 \times {10^{ - 19}}J\) et \(1nm = {10^{ - 9}}m\)
2-4.On considère un solénoïde, de résistance \(R = 10\Omega \), comportant N = 500 spires et de surface S = 3 cm2 . Ses bornes sont réunies par un fil de résistance négligeable. Ce solénoïde est placé dans un champ magnétique uniforme \(\overrightarrow B \) orienté suivant son axe, dans le même sens que \(\overrightarrow S \) et d’intensité \(B = 6,28 \times {10^{ - 3}}T\).
2-4-1. Calculer le flux magnétique à travers le solénoïde. 1 pt
2-4-2-Reproduire le schéma ci-dessous et représenter le vecteur champ magnétique au centre du solénoïde. 1 pt 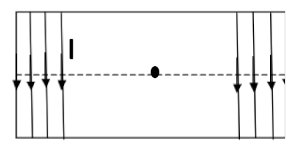 2-4-2. On annule le champ magnétique en 5 secondes, on constate l’apparition d’un courant induit dans le solénoïde.
2-4-2. On annule le champ magnétique en 5 secondes, on constate l’apparition d’un courant induit dans le solénoïde.
a) Expliquer l’existence de ce courant. 1 pt
b) Déterminer la f.é.m. induite moyenne. 1 pt
EXERCICE 3 : Utilisation des savoirs et des savoir-faire (8 points)
1. Point de fonctionnement 2,5 points
Les caractéristiques intensité-tension de deux dipôles sont représentées sur le graphe donner ci-dessous. 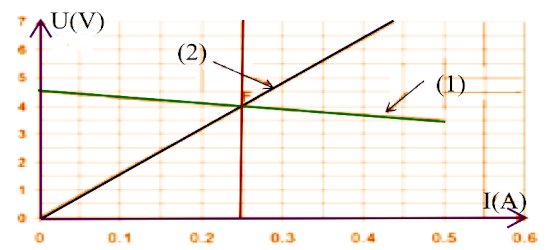 2.1 Faire le schéma du montage permettant d’obtenir ce graphe 1 pt
2.1 Faire le schéma du montage permettant d’obtenir ce graphe 1 pt
2.2 Déterminer le point de fonctionnement de ce circuit et en déduire les caractéristiques de ces dipôles 1,5 pt
2. Mécanique 3,5 points
Un solide de masse m se déplace dans une glissière constituée d’une partie rectiligne BC suivie d’une partie circulaire de centre O et de rayon R. Les frottements sont négligés. On donne g = 10 N/kg 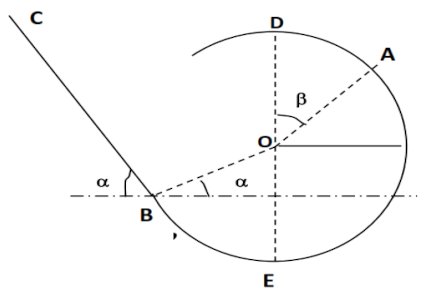 L’origine des altitudes est le plan horizontal passant par le point B. Le solide est lâché de C sans vitesse.
L’origine des altitudes est le plan horizontal passant par le point B. Le solide est lâché de C sans vitesse.
3-1-Exprimer l’énergie mécanique en A et en C en fonction des données 1pt
3-2-Exprimer la vitesse en A en fonction des données. Et calculer si
\(m = 100 g\), \(R = 0,5 m\) et \(BC = 2 m\), \(\alpha = 1,2rad\) ; \(\beta = 1,rad\) 1pt
3-3-La vitesse minimale en D doit être supérieure à \(\sqrt {10R} \) si non le point D n’est pas atteint.
3-3-1-Quel doit être l’énergie minimale en C permettant d’atteindre D ? 0,75 pt
3-3-2-En déduire l’altitude minimale de C permettant d’atteindre D. 0,75pt
3. Calorimétrie 2 points
Un morceau de fer de masse \({m_1} = 500g\) est sorti d’un congélateur à la température \({\theta _1} = - {30^o}C\), il est plongé dans le calorimètre de capacité thermique négligeable , contenant une masse \({m_2} = 200g\) d’eau à la température \({\theta _1} = - {4^o}C\). Déterminer l’état final du système (température d’équilibre thermique ; masse des différents corps présents dans le calorimètre
Données :
Chaleur massique du fer : \({C_{fer}} = 456J.K{g^{ - 1}}{k^{ - 1}}\);
-Chaleur massique de l’eau : \({C_{e}} = 4185J.K{g^{ - 1}}{k^{ - 1}}\) -Chaleur massique de la glace : \({C_{g}} = 2060J.K{g^{ - 1}}{k^{ - 1}}\);
Chaleur latente de fusion de la glace : \({l_{f}} = 456J.K{g^{ - 1}}{k^{ - 1}}\)
Partie B : Évaluation des compétences : 16 points
Situation problème 1 :
Au cours d’une séance de travaux pratiques, un groupe d’élève désire observer à travers un appareil d’optique un objet invisible à l’œil nu. Alim est un élève de ce groupe, il ne voit nettement que les objets situés entre 10 ?? et 2,5 ? . Il se plaint de n’avoir pas observé l’objet à travers cet appareil d’optique comme les autres. Pour l’aider, le moniteur lui propose de refaire la séance de travaux pratique seul et met à sa disposition un kit de lentilles, contenant six lentilles portant les inscriptions : \({L_1}:500\delta \) ; \({L_2}:1\delta \) ; \({L_3}:20\delta \) ; \({L_4}:2\delta \) ; \({L_5}:3\delta \) ; \({L_6}:-20\delta \). Alim doit choisir deux lentilles du kit et les monter sur l’appareil optique. Il doit ensuite bien régler l’appareil pour percevoir l’objet dans ses limites de visions distinctes.
L’appareil optique porte les indications suivantes : \(Pi = 2500\delta \); \({G_C} = 625\); \(\Delta = 15cm\).
Pour une bonne observation d’un l’objet à travers cet appareil, la distance entre les centres optiques des lentilles doit être \(? = 18,2 ??\) et l’œil doit être positionné au foyer principal image de l’oculaire.
A l’aider d’un raisonnement scientifique et logique et en utilisant les données ci-dessus, propose à cet élève les lentilles à utiliser pour bien percevoir cet objet à travers l’appareil optique.
Situation problème 2 :
Pour construire le dernier niveau d’un immeuble, un entre preneur à adapter la machine simple ci-dessous pour faire monter le matériel de construction suivant : poutres tissées en fer de masse commune 75 kg, récipient contenant 60 litres de béton de masse 252 kg et les panneaux préfabriqués de masse commune 648 kg 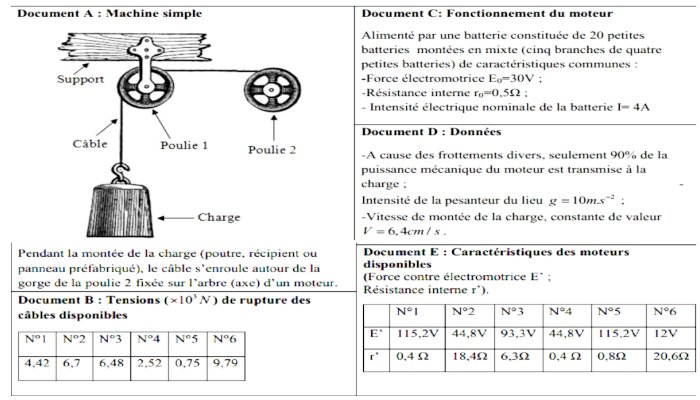 En exploitant les informations ci-dessus et en utilisant un raisonnement scientifique et logique, choisir les câbles et le moteur convenable de la machine simple, pour faire monter les charges.
En exploitant les informations ci-dessus et en utilisant un raisonnement scientifique et logique, choisir les câbles et le moteur convenable de la machine simple, pour faire monter les charges.

