Partie A : Évaluation des ressources / 15 points
Exercice I / 3 pts
1. Montrons que la probabilité pour qu'une équation caractéristique de (E) admette deux solutions réelles distinctes ou confondues est de 2936 1,5 pt
Une équation caractéristique r2+2ar+b=0 de (E) admet deux solutions réelles ou confondues si et seulement si 4a2−4b≥0, c'est-à-dire que a2≥b
Tableau de signes de 4a2−4b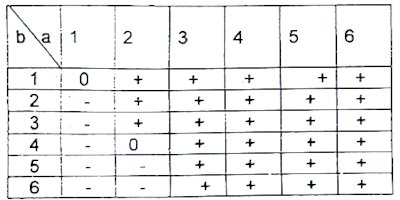 Il y'a 29 couples (a,b) qui vérifient a2≥b, sur un total de 36 Donc cette probabilité est égale 2936.
Il y'a 29 couples (a,b) qui vérifient a2≥b, sur un total de 36 Donc cette probabilité est égale 2936.
2. Déterminons le nombre de fois au minimum dont on doit répéter cette expérience pour être sûr d'avoirr au moins 98% de chances que l'équation caractéristique de (E) ait au moins une fois, deux solutions non réelles.
Désignons par n ce nombre de fois. Ainsi, on a un schéma de Bernoulli de n épreuves et dont la probabilité du succès est p=1−2936=736
Avoir au moins une fois deux solutions non réelles c’est, soit 1 fois jusqu’à n fois et dont la probabilité est ∑nk=1Ckn(736)k(2936)n−k
Il faut alors que ∑nk=1Ckn(736)k(2936)n−k≥98%. Ce qui est-équivalent à 1−C0n(2936)n≥98100.
D'où n≥ln50ln36−ln29=18,09. Donc le nombre minimum de fois de répéter cette expérience est 19. 1,5 pt
Exercice II / 03 pts
1. Déterminons une base du noyau (Kerφ) de φ, puis justifions que φ n'est pas bijectif.
Soit →u(x,y,z) un vecteur de E3.
→u∈Kerφ⇔φ(→u)=→0 ⇔{x+2y=02x+y+3z=0−x+y−3z=0 ⇒{x=−2yz=y.
Donc (−2→i+→j+→k) est une base du noyau (Kerφ) de φ.
. Puisque Kerφ≠{→0}, alors φ n'est pas bijectif. 1 pt
2.a Montrons que l'image (Imφ) de φ est un plan vectoriel de E3.
On a dim(Imφ)=dimE3 −dim(Kerφ)=2. Ainsi, Imφ est un sous espace vectoriel de E3 de dimension 2. Donc Imφ est un plan vectoriel de E3 0,5 pt
2.b *Vérifions que φ(→k)=2φ(→i)−φ(→j)
2φ(→i)−φ(→j)= 2(→i+2→j−→k)− (2→i+→j+→k)= 3→j−3→k=φ(→k) 0,5 pt
2.c. Déduisons-en une base de Imφ.
Imφ est engendrée par φ(→i), φ(→j) et φ(→k). Et donc par φ(→i) et φ(→j) d'après la question 2. b.
Par conséquent, (φ(→i), φ(→j)) constitue une base de Imφ qui est un plan vectorielle d après la question 2.a 1 pt
Exercice III / 04 pts
1. Déterminons le sens de variation de F sur [1;+∞[.
F est dérivable sur [1;+∞[ et pour tout x∈[1;+∞[, F′(x)=f(x) et f(x) est strictement positif sur [1;+∞[. Donc F est strictement croissante sur [1;+∞[. 0,25 pt
2.
a. Montrons que pour tout réel t≥0, t+2≥2√2√t.
Soit t−2√2√t+2= (√t−√2)2. D’où t−2√2√t+2≥0. Donc t+2≥2√2√t.0,25 pt
b. Déduisons-en que pour tout réel x≥1 , F(x)≤12√2 ∫x1(t+2)e1−tdt 0,5 pt
2.b soit x≥1 et t∈[1;x], d’après la question précédente (2.a), on a 2√2√t≤t+2. D’où x∫12√2√te1−tdt≤ x∫1(t+2)e1−tdt car e1−t≻0, ainsi 2√2x∫1√te1−tdt≤x∫1(t+2)e1−tdt d’où F(x)≤12√2x∫1(t+2)e1−tdt.
3.a. Montrons à l'aide d'une intégration par parties que x∫1(t+2)e1−tdt= 4−(x+3)e1−x
En définissant les fonctions u et v par u(t)=t+2 et v′(t)=e1−t, on a x∫1(t+2)e1−tdt= 4−(x+3)e1−x . 0,5 pt
3.b. Déduisons-en' que pour tout réel x≥1, 0≤F(x)≤√2
Soit un réel x≥1. .
D'une part, pour tout x≥1, f(x)≻0. D'où F(x)≥0
D'autre part, d'après la question 2.b., F(x)≤12√2x∫1(t+2)e1−tdt et d’après la question 3.a.
On a F(x)≤12√2(4− (x+3)e1−x) D'où F(x)≤42√2 car (x+3)e1−x≻0. Ainsi F(x)≤√2
Donc pour tout réel x≥1, F(x)≤√2 0,5 pt
4.1. Étudions le sens de variation de la fonction f sur [0;+∞[. 0,5 pt
f est dérivable sur [0;+∞[ et pour tout x≻0, f′(x)=e1−x2√x(1−2x). Donc f est strictement croissante sur [0;12], et strictement décroissante sur ]12;+∞[.
2. Montrons que pour tout entier naturel n, f(n+1)≤un≤f(n)
Soient n un entier naturel non nul et un réel t∈[n;n+1]
Ainsi n≤t≤n+1, ce qui .entraine f(n+1)≤f(t)≤f(n) car f est .décroissante sur ]12;+∞[ qui contient [n;n+1]. D’où n+1∫nf(n+1)dt≤ n+1∫nf(t)dt≤n+1∫nf(n)dt
Donc f(n+1)≤n+1∫nf(t)dt≤f(n)
43. (i) Déduisons-en que la suite u est décroissante.
Soit n un entier naturel.
f(n+2)≤un+1≤f(n+1) et f(n+1)≤un≤f(n) d’après la question 4.2.
Ainsi un+1≤un.
Donc la suite (un) est décroissante.
4.3. (ii) Déduisons-en que la suite u est convergente. 0,5 pt
limx→+∞f(x)=limx→+∞x12ex=0 d'après les croissances comparées. D'où ' limx→+∞f(n)=limx→+∞f(n+1), ainsi limx→+∞un=0. Donc la suite u est convergente.
N.B : On remarque aussi que la suite u est décroissante et minorée par 0. Donc converge.
Exercice IV / 05 points
1. Montrons que l’équation de (Γ) peut encore s'écrire : (x−1)2α−y2β=1 ou α et β sont deux réels strictement positifs que nous déterminerons. 1 pt
Soit M(x;y) un point du plan complexe rapporte au repère (O;→u,→v). 1 pt
M(x,y)∈(Γ)⇔ 3x2−y2−6x−1=0
3x2−y2−6x −1=0⇒3(x−1)2 −y2=4 ⇒ (x−1)243−y24=1
Donc α=43 et β=4
2. Déduisons-en que (Γ) est une hyperbole dont nous déterminerons le centre et les sommets par leurs coordonnées dans le repère (O;→u,→v) 1 pt
• (Γ) est une hyperbole de par la forme de son équation réduite.
• Les coordonnées de son centre sont : (1;0).
• Les coordonnées des sommets sont (2√33+1,0) et (−2√33+1,0)
3. Déterminons la demi distance focale et l’excentricité de (Γ) 0,5 pt
• La demi-distance focale est √43+4=4√33
• L'excentricité est 4√332√33=2
4.1 Donnons la nature et les éléments caractéristiques de S. 1 pt
Nature : S est une similitude plane directe.
Éléments caractéristiques : rapport = 2 ; angle π6 (modulo 2π) ; centre d'affixe : 1−√3+i1−2eiπ6=1
4. 2.a. Montrons que N est l'image de M par une transformation du plan dont nous donnerons la nature et les éléments caractéristiques. 1 pt
On a IN=2IM et Mes(→IM;→IN)=π6 deux ëgalités montrent que N est l'image de M par la similitude directe plane de centre I, de rapport 2 et d'angle π6, Il s'agit de la similitude S.
4. 2. b. Déduisons-en la nature de l'ensemble (Γ′) décrit par N lorsque le point M décrit l’ensemble (Γ), puis précisons l’excentricité de (Γ′). 0,5 pt
(Γ′) est une hyperbole.
Son excentricité est égale 2.
Partie B : Évaluation des compétences 05 points
Tâche 1 : Déterminons le temps minimum après lequel on doit administrer ce produit aux maquereaux.
• Déterminons la quantité Qn de maquereaux dans l'étang 1 après n mois.
Les quantités Qn sont des termes d’une suite géométriques de premier termes Q0=250 et de raison 1,2 : Qn=250×(1,2)n
• Déterminons le minimum de mois après lesquels cette quantité aura au moins doublé.
Cette-quantité aura au moins doublé si et seulement si Qn≥2×Q0
Dou 250×(1,2)n≥2×250 ainsi n≥ln2ln1,2=3,8
Donc, c’est après au moins 4 mois qu’on doit administrer ce produit aux maquereaux.
Tâche 2 : Déterminons le temps minimum après lequel on doit administrer ce produit aux carpes.
• Déterminons la quantité Q(t) carpes dans l'étang 2 après t mois.
La vitesse d’accroissement Q′(t) des carpes à un instant t étant le cinquantième de leur quantité Q(t) au même instant, alors Q′(t)=15Q(t).
D'où Q(t)=ke150t et puisque Q(0)=450 Alors Q(t)=450e150t
• Déterminons le minimum de mois après lequel cette quantité aura au moins doublé.
Cette quantité aura au moins doublé si et seulement si Q(t)≥2Q(0)
D'où 450e150t≥2×450, ainsi t≥50ln2, c'est'-à-dire t≥34,65.
Donc, c'.est après au moins» 35 mois qu'on doit administrer ce produit aux carpes.
Tâche 3 : Vérifions si le restaurateur a au moins une chance sur deux de servir les deux clients dans l'ordre des commandes passées.
En suivant la consigne principale de ce restaurant-qui consiste à servir les clients-dans l'ordre de passage de leurs commandes (voir situation), la probabilité de servir des deux clients dans l'ordre des commandes passées est 1.
Le restaurateur a ainsi 100% de chance de servir ces -clients dans l'ordre. Donc au moins une chance sur deux.
N.B. Le texte lié à cette tâche présente des données superflues et quelques insuffisances.

