EXERCICE I Les lois de Newton
Exercice I
Les équations horaires des mouvements des solides sont:
a){x(t)=2t+1y(t)=4t+3
b){x(t)=2ty(t)=t2+3t
c){x(t)=2cos(ωt)+2y(t)=2sin(ωt)−1
d){x=ty=√4−t2
Dans chaque cas,
1) Dire lequel des mouvements est plan.
2) Déterminer la nature de sa trajectoire
3) Déterminer le vecteur vitesse et son intensité.
4) Calculer la norme du vecteur vitesse à t= 5s.
5) En déduire les composantes normales et tangentielles de l’accélération dans la base de Frenet.
6) En déduire les composantes cartésiennes du vecteur accélération.
7) Montrer que le module de l’accélération est indépendant du repère d’étude.
8) Calculer la norme du vecteur accélération à t= 5s.
EXERCICE II Les lois de Newton
Exercice II
La vitesse v(t) d’un mobile est représentée sur la figure ci-dessous en fonction du temps t.
1. Donner l’expression de la vitesse en fonction du temps.
2. Quel est le graphe représentant l’accélération du mobile en fonction du temps ?

Graphe 1

Graphe 2.

Graphe 3
3. Quelle est la condition pour qu’un mouvement soit accéléré, retardé ou uniforme dans un intervalle donné?
EXERCICE III Les lois de Newton
Exercice III
Un solide S de masse m=400g, abandonné avec une vitesse initiale v0, glisse le long de la ligne de plus grande pente d’un plan incliné d’angle α=300 par rapport au plan horizontal. Un dispositif approprié permet d’enregistrer quelques positions successives Gi de son centre d’inertie G, à des dates ti régulièrement espacées tel que ti+1−ti=200ms
L’origine des dates correspond à la position Go. On néglige les dimensions de S et on prend g=10 m.s-2. 1– Compléter le tableau suivant:
1– Compléter le tableau suivant:
| Gi | G0 | G1 | G2 | G3 | G4 | G5 |
| ti(s) | 0 | |||||
| xi(cm) | 0 | |||||
| vi(cm/s) | v0 | × | ||||
| ai(cm/s2) | × | a1 | × | × |
On admettra que: →vi=→Gi−1Gi+1ti+1−ti−1 et →ai=→vi+1−→vi−1ti+1−ti−1
2. Tracer sur un papier millimètre le graphe vG=f(t). On prendra pour échelles:1cm↔0,1s et 1cm↔0,2m/s
3. Déduire de cette courbe :
3.1 La valeur v0 de la vitesse qu’avait le solide au départ du point G0.
3.2 La valeur de l’accélération du centre d’inertie G.
4 Par application du théorème du centre d’inertie au solide, déterminer la valeur théorique de l’accélération du solide S.
5. Comparer les valeurs de l’accélération du centre d’inertie du solide obtenues en 1, 3 et 4. puis conclure.
6. Calculer l’intensité des forces de frottement
EXERCICE IV Les lois de Newton
Exercice IV
Un solide A de masse mA=3kg peut glisser le long de la ligne de plus grande pente d’un plan incliné d’angle α=300. il est relié par deux fils fins qui passe par les gorges de deux poulies de masses négligeables et de rayons R au bout desquels sont attachées deux masses mB=4kg et mB’=2kg (voir schéma ci-contre).
Le système, abandonné à lui-même lorsque le solide A est en O prend un mouvement uniformément accéléré. g=10N/kg
1. Calculer l’accélération aG de A.
2. Calculer les intensités des tensions T’A et TA des fils AB et AB’.
3. Calculer le temps mis par le solide A pour aller de O à S si OS=2m, puis sa vitesse au point S.
EXERCICE V Les lois de Newton
Exercice V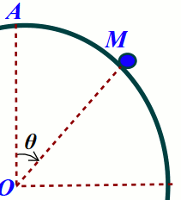
Un solide (S) de masse m, assimilable à un point matériel, peut glisser sans frottement sur une gouttière ayant la forme d’un quart de cercle de centre O et de rayon r. On le déplace légèrement de sorte qu’il quitte le sommet A avec une vitesse nulle. Une position M de (S) à un instant t est repérée par l’angle θ que fait le rayon OP avec le rayon OA.
1.Reproduire le schéma et représenter les forces exercées sur (S) au point M.
2. Appliquer, au point P, la deuxième loi de Newton au système (S), et en déduire les expressions de :
2.1 La composante tangentielle aτ du vecteur accélération en fonction de g et θ.
2.2 Le module R de la réaction de la gouttière en fonction de m, g , θ et de la vitesse v au point M.
3. En appliquant le théorème de l’énergie cinétique au système (S) entre l’instant où il quitte A et celui où il se trouve au point M, exprimer le module du vecteur vitesse de (S), en fonction de g , θ et r.
4. En déduire l’expression de R en fonction de g, θ et m.
5. Déterminer, en degré, la valeur de l’angle θ lorsque le solide ( S ) quitte la gouttière.
EXERCICE VI Les lois de Newton
Exercice VI
Un objet de masse m est suspendu par un fil de masse négligeable. Le fil est enroulé autour d’un disque plein (poulie) de rayon r et de masse M tournant sans frottement autour d’un axe horizontal D.
À l’instant t=0, l’objet est abandonné sans vitesse initiale au point O. La position de l’objet est repéré par son abscisse x mesurée à partir de O .L’axe Ox est orienté positivement vers le bas. (voir figure ci-contre).
On donne m=1kg, M=1kg, r =20cm. Le moment d’inertie par rapport à l'axe de rotation de la poulie est: JΔ=12Mr2. On prendra l’accélération de la pesanteur égale à g=9,8m.s-2.
1-Faire un bilan des forces qui s’exercent
1.1 Sur l’objet
1.2 Sur la poulie
2-En appliquant le théorème du centre d’inertie à l’objet d’une part et le théorème de centre d’inertie d’un solide en rotation autour d’un axe à la poulie d’autre part, donner les expressions en fonction de m, M et g:
2.1 De l’accélération aG de l’objet suspendu. Faire l’application numérique
2.2 De la tension du fil.
4-Déterminer la date t pour laquelle la vitesse angulaire de la poulie devient égale à 10 rad.s-1.
5-Donner les équations horaires x(t) de l’objet et θ(t) de la poulie. Quelles sont les natures des mouvements :
5.1 De l’objet.
5.2 De la poulie.
EXERCICE VII Les lois de Newton
Exercice VII
Une bille est lancée sur un plan incliné d’un angle α=100 par rapport à l’horizontale. Un dispositif approprié permet d’enregistrer ses positions successives qui sont représentées sur la figure ci-dessous.
1. Déterminer les intensités des vecteurs →v2 et →v4 représentant les vitesses de la bille aux points G2 et G4.
2. Déterminer l’accélération de la bille au point G3.
Les enregistrements se font à intervalle de temps régulier:ti+1−ti=50ms
EXERCICE VIII Les lois de Newton
Exercice VIII
La charge élémentaire fut déterminée pour la première fois en 1911 par le physicien américain Robert Andrews Millikan. Dans son expérience, Millikan injecte à l'aide d'un vaporisateur de petites gouttelettes d'huile entre deux plaques métalliques horizontales A et B, entre lesquelles est appliquée une tension électrique UAB=4,31kV. Ces gouttelettes ont été préalablement chargées en les exposant à des rayons X.
Or des particules chargées, de charge q, placées entre deux plaques soumises à une tension UAB séparées d'une distance D=20,0 mm, sont soumises à la force électrique Fe. On observe, dans l'expérience de Millikan, que pour une certaine valeur de UAB, les gouttelettes sont en équilibre : elles sont donc immobiles.
On observe, dans l'expérience de Millikan, que pour une certaine valeur de UAB, les gouttelettes sont en équilibre : elles sont donc immobiles.
La valeur Fe de cette force est telle que : Fe=qUABd, sa direction est perpendiculaire aux plaques.
a) Calculer le volume d'une goutte d'huile et en déduire sa masse.
b) Montrer que la goutte est soumise à son poids P=1,38.l0−13N.
c) Rappeler le principe d'inertie.
d) Vérifier que la poussée d'Archimède exercée par l'air peut être négligée.
e) A partir du texte, représenter les forces exercées sur la gouttelette sans souci d'échelle et en déduire la valeur de Fe.
f) En déduire la valeur de la charge élémentaire e en admettant que la charge d'une gouttelette d'huile est q = 4e.
Données :
Volume d'une sphère de rayon V=34πr3
Intensité de la pesanteur: g = 9,81 N/kg
Rayon de la goutte : r = 1,58. 10−3mm
Masse volumique de l'huile: ρhuile=829kg/m3.
Masse volumique de l'air : ρhuile=1,29kg/m3.

