I– Aspect ondulatoire de la lumière Correction des exercices sur la lumière
Exercice I
1.1L’effet photoélectrique est l’extraction des électrons d’un métal lorsqu’il est convenablement éclairé par un rayonnement électromagnétique.
1.2 Représentation 1.3 Schéma
1.3 Schéma 2.1 Détermination de la longueur d’onde seuil : W0=hCλSW0=hCλS ⇒⇒λS=hCW0λS=hCW0
2.1 Détermination de la longueur d’onde seuil : W0=hCλSW0=hCλS ⇒⇒λS=hCW0λS=hCW0
C’est la longueur d’onde inférieur à la longueur d’onde seuil qui permet l’effet photoélectrique: soit λ=430nm.
2.2 Calcule de la vitesse maximale des électrons : 12mev2=12mev2= hϑ−W0hϑ−W0 soit v=√2(hCλ1−W0)mev=√2(hCλ1−W0)me v=0,414106m/sv=0,414106m/s
2.3 C’est le potentiel minimal permettant de donner aux électrons une énergie suffisante pour quitter le métal
Calcule du potentiel d‘arrêt
D’après le théorème de l’énergie cinétique
Le travail de la force électrique est résistant : ECA−ECC=ECA−ECC= 0−12mev2 =W(→F) =−(−e)U0 U0=−me.v22.e U0=−0,49V
I-1 Interférences lumineuses Correction des exercices sur la lumière
Exercice II
1. Calcule de la position de la frange centrale. La frange est centrale si d1 = d2 , de la différence de marche δ=d2−d1 =axD=0 ⇒x=0
La frange est centrale si d1 = d2 , de la différence de marche δ=d2−d1 =axD=0 ⇒x=0
La frange centrale est à la position O
2. L’amplitude maximale est obtenue pour: δ=d2−d1 =kλ, Soit : x=kλDa=k.i Nous avons donc :
| k | -2 | -1 | 0 | 1 | 2 |
| x | -2i | -i | 0 | i | 2i |
3. L’interfrange est donné par : i=λDa i=0,6mm
4. Calcule de la position de la frange centrale par rapport à O. 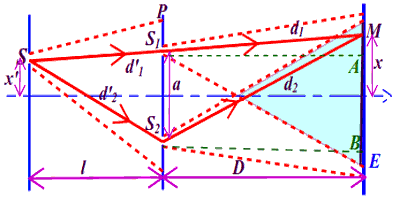 δ=(S′S2+S2M) −(S′S1+S1M) =(S′S2−S′S1) +(S2M−S1M) =(d′2−d′1) +(d2−d1)
δ=(S′S2+S2M) −(S′S1+S1M) =(S′S2−S′S1) +(S2M−S1M) =(d′2−d′1) +(d2−d1)
Nous avons montré que : d2−d1=axD
On montre de la même façon que, avec : l≻≻a et l≻≻x′, d′2−d′1=2l, d′2−d′1=ax′D. Ainsi, δ=ax′D+ axD=aD(x+x′)
Les franges brillantes sont obtenues pour la différence de marche égale aux valeurs entières de la longueur d’onde. δ=ax′D+ axD= =kλaD(x+x′) soit x+x′=kλDa
La frange centrale est obtenue pour k=0... Ainsi : x=−x′=−1mm Parce que nous avons déplacé la source S’vers le haut, le point M est en dessous de O.
Si on avait déplacé la source S’ vers le bas, le point M aurait été au dessus de O.
La frange centrale est toujours déplacée du coté opposé à celui se S’. La valeur de l’interfrange ne change pas
5. Calcule de la position de la frange centrale par rapport à O La vibration en M issue de S1 a parcouru une longueur e dans la lame et d1 - e dans l’air. La célérité de la lumière dans l’air est C et C’ dans la lame. n=CC′ et eC′=e.nC
La vibration en M issue de S1 a parcouru une longueur e dans la lame et d1 - e dans l’air. La célérité de la lumière dans l’air est C et C’ dans la lame. n=CC′ et eC′=e.nC
Le temps mis pour aller de S1 à M est : t=t1+t2= eC′+ d1−eC= e.nC+ d1−eC
La distance parcourue par le rayon lumineux est donc : d′1=Ct =(t1+t2) =en+d1−e =d1+e(n−1)
La différence de marche est donc : δ=d2−d′1 =d2−d1 −e(n−1) δ=a.xD−e(n−1)
L’amplitude maximale est obtenue pour : δ=a.xD −e(n−1) =kλ x=Da(kλ+e(n−1))
La frange centrale est obtenue pour k=0, soit : x=Dae(n−1)
La frange centrale se déplace du coté de la lame.
Exercice III
1. Le travail d'extraction de l’électron vaut : W0=hϑS=hCλS soit W0=310−19J =310−191,610−19 =1,9eV
2.1 Déterminons l’énergie cinétique d’un électron émis par la cathode EC=hCλ−W0 EC=1,510−19J
2.2 Calcule de la vitesse de cet électron : 12mev2=EC v=√2ECme v=√2.1,5×10−199,1×10−31 =0,58×106m/s
3.1 Déterminons la sensibilité de la cellule ; IS=σ.P σ=ISP σ=5,5×10−3A/W
3.2 Calculons le rendement quantique de la cellule ; {P=N.EIS=n.e ⇒r=nN.100 =ISePE.100 ainsi, r=IS.Ee.P.100 r=IS.h.ϑe.P.100 r=1,26%
II– Aspect corpusculaire de la lumière Correction des exercices sur la lumière
Exercice IV
1. Calcule de la vitesse des électrons. 12mev2= −(−e)UAC v=√2eUACme v=5,9×105m/s
2.1 r=nN où n est le nombre de photons efficaces (ceux qui arrachent des électrons) et N le nombre total de photons reçus par la cathode en 1seconde, IS=r.e.Ph.ϑ0 IS=2,710−5A
II.1 Expérimentation Correction des exercices sur la lumière
Exercice V
1. Traçons la courbe On obtient une droite d’équation : ϑ(|U0|)= 2,42×1014|U0| +5,33×1014
On obtient une droite d’équation : ϑ(|U0|)= 2,42×1014|U0| +5,33×1014
2. Déterminons la valeur seuil photoélectrique. Nous avons montré que : EC=eU0 =hϑ−W0 ⇒ ϑ(|U0|)= ehU0+W0h qui est l’équation de la droite précédente.
D’après l’équation ci-dessus, le seuil photoélectrique correspond à l’ordonnée à l’origine de la droite. ϑ0=5,33×1014Hz
Calculons à partir de cette valeur l’énergie d’extraction : W0=hϑ0 W0=3,5×10−19 =3,5×10−191,6×10−19 =2,197eV, Il y a dont compatibilité.
3. Déterminons la constance de Planck à partir de la courbe. En effet. La pente de la courbe est : a=tan(θ) =ΔϑΔ|U0| =2,421014 =eh soit h=e2,42×1014 =6,611×10−34J.s Ce qui est très proche de la valeur admise.
II.2 Caractéristique photoélectrique Correction des exercices sur la lumière
Exercice VI
1. Calcule du nombre d’électrons émis. IS=ne ⇒ n=ISe soit n=10×10−61,6×10−19 =6,25×1013 _\'electrons
2. Calcule du nombre de photons éclairant la cathode par seconde si le rendement est r=0,01. r=nN N=nr N=6,25×1015 _photons
3. L’énergie lumineuse reçue par la cathode pendant une seconde est : E=hϑ=h.Cλ E=4,19×10−19J
4. Calcule de la puissance lumineuse reçue :P=N.E P=3,10×10−3W
5. Expression du rendement : r=IS.h.ϑe.P.100
II.3 Le potentiel d’arrêt Correction des exercices sur la lumière
Exercice VII
1. Calcule de l’interfrange : i=λDa i=1,4×10−3m
2.1 On a montré que : δ=d2−d′1 =d2−d1 −e(n−1) =a.xD−e(n−1)
2.2 L’augmentation de l’épaisseur de la lame entraine le déplacement progressif de la frange centrale ainsi que toutes les autres franges du coté de la lame.
2.3 Calcule de e-e0
Les deux différences de marche s’écrivent δ=a.xD− e(n−1) et δ′=a.x′D −e0(n−1)
La frange centrale en O a laissé la place à la frange noire alors : δ=kλ et δ′=(2k+1)λ2 Soit δ−δ′=λ2 de plus, 9 franges brillantes ont défilé alors x’-x=9i. Nous avons donc : δ−δ′=a(x−x′)D −(n−1)(e−e0) =λ2 ⇒ e−e0= a(x−x′)D(n−1)− λ2(n−1)= 9a.iD(n−1)− λ2(n−1)
2.4.1 On observe à l’écran un spectre cannelé.
2.4.2 Calcule des longueurs d’onde des radiations complètement éteintes. L’ordre d’interférence est donné par : P=δλ= 6×10−6λ ⇒ λ=6×10−6P
Pour le spectre visible, on a : ,4×10−6≤ 6×10−6P≤ 0,75×10−6 soit 60,75−12≤ k≤ 60,4−12
| k | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| P | 8,5 | 9,5 | 10,5 | 11,5 | 12,5 | 13,5 | 14,5 |
| λ(×10−6)m | 0,7 | 0,63 | 0,57 | 0,52 | 0,48 | 0,44 | 0,41 |

