Partie A : Évaluation des ressources (10 points)
Activités numériques (5 points)
Exercice 1 : (2,5 points)
1. Un groupe d’enfants se partage équitablement 3 007 oranges et 2 813 pamplemousses.
a) Trouve le nombre maximal d’enfants faisant partie de ce groupe. 0.75pt
b) Combien d’oranges puis de pamplemousses chaque enfant du groupe a-t-il reçu ? 0.5pt
2. Écris le nombre (2+√5)2−3√20 sous la forme a+b√5 où 𝑎 et 𝑏 sont des entiers. 0.75pt
3. Relève le numéro de cette question suivi de la lettre choisie correspondant à réponse juste.
L’ensemble des solutions de l’équation (2x−6)2=0 est :
a) S={3};
b) S={−3;3};
c) S={−32;32} ;
d) S={−√3;√3} 0.5pt
Exercice 2 : (2.5 points)
1. Développe, réduis et ordonne le polynôme 4x2−(2x+1)(−x+1) 0.75pt
2. Prouve que l’application linéaire donnée par 𝑓(𝑥)=−3𝑥 est décroissante. 0.25pt
3. Calcule la taille moyenne des données statistiques du tableau ci-dessous. 0.5pt
| Taille (en ) | 1,5 | 1,6 | 1,7 | 1,8 | 1,85 | Total |
| Effectifs | 4 | 10 | 8 | 10 | 8 | 40 |
4. Résous par substitution dans R×R le système d’équations : {a+b=364a+2b=90 1 pt
Activités géométriques (5 points)
Exercice 1 : (2.75 points)
Sur le schéma ci-contre, 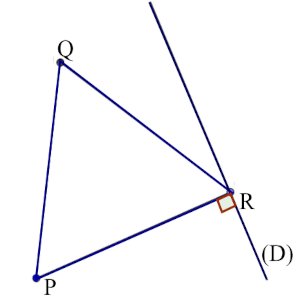 𝑃𝑄𝑅 est un triangle équilatéral de 6 𝑐𝑚 de côté ; la droite (𝐷) est perpendiculaire à la droite (𝑃𝑅) .
𝑃𝑄𝑅 est un triangle équilatéral de 6 𝑐𝑚 de côté ; la droite (𝐷) est perpendiculaire à la droite (𝑃𝑅) .
1.a) Place le point d’intersection F des droites (𝑃𝑄) et (𝐷) . 0.25pt
b) Montre que cos^FPR=12 0.25pt
c) Déduis-en que 𝑄 est le milieu du segment [𝑃𝐹]. 0.25pt
2. La perpendiculaire à la droite (𝐹𝑅) en E passant par Qcoupe au point K le demi-cercle de diamètre [𝑃𝐹] contenant le point R.
a) Montre que (𝑄𝐾) est la médiatrice du segment [𝐹𝑅]. 0.5pt
b) Calcule la longueur 𝐹𝑅 . 0.5pt
c) Recopie et complète le tableau suivant : 0.5pt
| Angles |
^QRE |
^FKR |
| Mesures en degré |
d) Déduis-en que le quadrilatère 𝑄𝐹𝐾𝑅 est un losange. 0.5pt
Exercice 2 : (2.25 points)
On considère un triangle équilatéral ABC de centre O et de côté 9 cm.
On désigne par E, F, G, H, I et J les points des trois côtés de ce triangle tels que AE = BF = BG = CH = CI = AJ = 3cm comme l’indique la figure suivante. 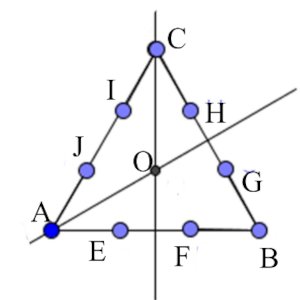 1. Montre que JE=GH=3 cm et que (JE)//(GH). 0.75pt
1. Montre que JE=GH=3 cm et que (JE)//(GH). 0.75pt
Et de manière analogue, on accepte que FG = IJ = 3 cm et IH = EF = 3 cm.
2. Montre que (OA) est la médiatrice des segments [JE] et [GH]. 0.75pt
Et de manière analogue, on accepte que (OB) est la médiatrice des segments [FG] et [IJ] et que (OC) est la médiatrice des segments [IH] et [EF].
3. Déduis-en que le polygone EFGHIJ est inscriptible dans un cercle. 0.5pt
4. Déduis de 1) et 3) la nature exacte du polygone EFGHIJ. 0.25pt
Partie B : Évaluation des compétences (10 points)
Situation :
Lors de la construction de la route reliant Maroua et Mora, deux villes de la région de l’Extrême-Nord au Cameroun, deux camions-bennes quittent au même moment un lieu B de la ligne de chaussée à revêtir pour aller ramasser un tas de graviers assimilable à un cône de révolution de 14 m de diamètre et 21 m de hauteur dans une carrière située à un endroit A pour revenir déposer au lieu B.  Le camion-benne n°1 se déplace à la vitesse moyenne de 60km/h tandis que le camion-benne n°2 roule à la vitesse moyenne de 50km/h. Ces vitesses ont été calculées en incluant le temps de chargement et déchargement.
Le camion-benne n°1 se déplace à la vitesse moyenne de 60km/h tandis que le camion-benne n°2 roule à la vitesse moyenne de 50km/h. Ces vitesses ont été calculées en incluant le temps de chargement et déchargement.  Et chaque benne des camions a les caractéristiques suivantes : 8 m sur 2,5 m de surface de base et 3 m de hauteur.
Et chaque benne des camions a les caractéristiques suivantes : 8 m sur 2,5 m de surface de base et 3 m de hauteur.
Zède ayant exploité une carte de la région de l’Extrême-Nord dans laquelle sont placés dans un repère orthonormé d’unité un kilomètre, les points A et B, conclut que la carrière est à une demi-dizaine de kilomètres de lieu de revêtement de la chaussée. Les schémas ci-contre illustrent ces situations. 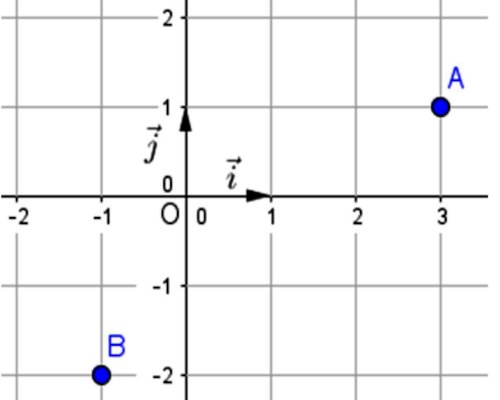 Prendre π=227
Prendre π=227
Tâches :
1. Détermine le nombre de tours réunis qu’auraient fait les deux camions-bennes pour terminer de ramasser le tas de graviers. 3 pts
2. Montre que Zède a raison. 3 pts
3. Détermine le temps mis pour lequel les deux camions-bennes pourraient pour la première fois, verser au même moment du gravier au lieu de revêtement de la chaussée. 3 pts
Présentation : 1 pt

