Partie A : Évaluation des ressources /24 points

Exercice 1 : vérification des savoirs/8 points

1- Définir : effet photoélectrique, onde mécanique. 2pts
2- Donner les unités SI des grandeurs physiques suivantes : période radioactive, champ magnétique. 1pt
3- Énoncer la troisième loi de newton. 1pt
4- Donner une interprétation physique de l’état d’un point immobile du champ d’interférences1pt
5- Citer deux applications de l’effet doppler. 1pt
6- Choisir la bonne réponse (QCM) 0,5x3=1,5pt
6.1- Dans le repère de Frenet, \(\overrightarrow n \) est un vecteur unitaire
A) orthogonal à \(\overrightarrow \tau \) et orienté vers l’intérieur de la trajectoire
B) orthogonal à \(\overrightarrow \tau \) et orienté dans le sens du mouvement;
C) orthogonal a \(\overrightarrow \tau \) et orienté vers l’extérieur de la trajectoire.
6.2- La période propre des oscillations d’un pendule de torsion de moment d’inertie \({J_\Delta }\) et de constante de torsion \(C\) s’écrit :
A) \({T_0} = 2\pi \sqrt {\frac{C}{{{J_\Delta }}}} \)
B) \({T_0} = 2\pi \sqrt {\frac{{mC}}{{{J_\Delta }}}} \)
C) \({T_0} = 2\pi \sqrt {\frac{C}{{m{J_\Delta }}}} \)
D) \({T_0} = 2\pi \sqrt {\frac{{{J_\Delta }}}{C}} \)
6.3- On donne la figure ci-après constituée de deux ressorts de raideurs \({K_1}\) et \({K_2}\) et d’un solide
A de masse m. Déterminer la période des oscillations de la masse m glissant sans frottement sur le plan horizontal.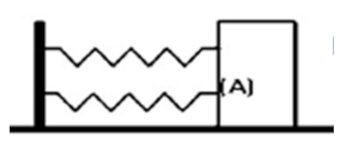
a) \(T = 2\pi \sqrt {m\frac{{{K_1} + {K_2}}}{{{K_1}{K_2}}}} \)
b) \(T = 2\pi \sqrt {\frac{m}{{{K_1} + {K_2}}}} \)
7- Donner le symbole d’une thermistance. 0,5pt

Exercice 2 : Application des savoirs et des savoir-faire/8 points

1- Généralités sur les systèmes oscillants : 4 points

Les oscillogrammes \({y_1}\) et \({y_2}\) ci-dessous sont ceux enregistrés au cours d’une expérience avec deux oscillateurs harmoniques.
1.1. Déterminer à partir du graphique, la période et l’amplitude de chaque fonction. 0,5ptx4 = 1pt
1.2. Exprimer le décalage horaire \(\theta \) comme une fraction de la période \(T\). 0,5pt
1.3. Laquelle des deux fonctions est en avance sur l’autre? Justifier. 0,5pt +0,5pt
1.4. En déduire la différence de phase \(\Delta \varphi = {\varphi _2} - {\varphi _1}\) entre ses deux fonctions. 0,5pt

2- Pendule pesant / 2 points

Une tige homogène de masse \(m= 0,5 kg\) et de longueur \(L= 2,0 m\) est mobile autour d’un axe
\(\left( \Delta \right)\) passant par l’une de ses extrémités. Le moment d’inertie de la tige par rapport à un axe passant par son milieu O est \({J_O} = 0,167\) ??/?².
2.1. Calculer le moment d’inertie \({J_\Delta }\) par rapport à l’axe \(\left( \Delta \right)\).
2.2. Déterminer la période des oscillations de faibles amplitudes de ce pendule pour \({J_\Delta } = 0,667kg/{m^2}\)
Donnée : g = 10 m/s² 1pt

3- Effet photoélectrique/ 2 points

Une cellule photoélectrique comporte une cathode (C) constituée d'une surface métallique dont la fréquence seuil est \({N_0} = 4,6 \times {10^{14}}\) Hz.
Un dispositif expérimental permet d'éclairer \((C)\) avec l'une des radiations de longueur d'onde : \({\lambda _1} = 560,0nm\) et \({\lambda _2} = 700,0nm\)
3.1. Déterminer la valeur \({\lambda _0}\) de la longueur d'onde du seuil photoélectrique. 1pt
3.2. Donner la (les) longueur (s) d’onde qui peut extraire des électrons du métal et leur communiquer une énergie cinétique. Donnée : célérité de la lumière \(c = 3 \times {10^8}m/s\). 1pt

Exercice 3 : Utilisation des savoirs /8 points

1. Mouvement dans les champs de pesanteur et électrique uniformes / 5 points

Une sphère de masse m et de charge \(q \prec 0\), considérée comme ponctuel, est lâchée en A sans vitesse initiale. Il glisse le long d’un tremplin ABC (voir figure 1).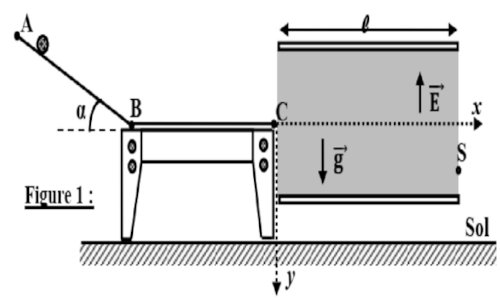
Les forces de frottements tout au long du trajet ABC sont assimilables à une force unique de valeur constante \(f\).
On admettra que le passage de la sphère au point B ne modifie pas la valeur de sa vitesse.
Données : \(m = 10 g\); \(f = {10^{ - 2}}N\); \(\alpha = {30^o}\); \(q = - {10^{ - 3}}C\); \(AB = BC\)\( = L = 50 cm\) ; g = 10 m/s2 ; \( ℓ = 0,2 m\)
1.1 Déterminer :
1.1.1. L’accélération \({a_1}\) de la sphère entre A et B et l’accélération \({a_2}\) de la sphère entre B et C. 0,5ptx2
1.1.2. La valeur de sa vitesse \({V_B}\) au point B et la valeur de sa vitesse \({V_C}\) au point C. 0,5ptx2
1.2. Au-delà du point C, la sphère quitte la table avec une vitesse \({V_B}\) = 1,7 m/s et évolue dans un espace où règnent simultanément deux champs uniformes : le champ de pesanteur et le champ électrique.
On étudie le mouvement de la sphère dans le repère orthonormé \((Cx, Cy)\).
1.2.1. En appliquant la deuxième loi de Newton, montrer que le vecteur accélération du mouvement de la sphère a pour composante: \({a_x} = 0\) et \({a_Y} = g - \frac{{qE}}{m}\) 1pt
1.2.2. Établir les équations horaires du mouvement de la sphère. 1pt
1.2.3. En déduire l’expression littérale de l’équation cartésienne de sa trajectoire. 0,5pt
1.2.4. Déterminer la valeur du champ \(\left( {\overrightarrow E } \right)\) pour que la sphère sorte de l’espace au point S d’ordonnée \({Y_S} = 12\) cm. 0,5pt

2. Mouvement dans un champ magnétique uniforme/3 points

A l’aide du spectrographe ci-contre, on se propose de séparer les ions \({}^6L{i^ + }\) et \({}^7L{i^ + }\) de masses respectives \({m_1}\) et \({m_2}\). Les ions pénètrent en \({O_1}\) dans le champ électrique uniforme existant entre les deux plaques verticales \({P_1}\) et \({P_2}\) pour y être accélérés jusqu’en \({O_1}\).
2.1. Donner le signe de la tension \(U = {V_{{P_1}}} - {V_{{P_2}}}\) que l’on établit entre \({P_1}\) \({P_3}\)? 0,5 pt
2.2. Les ions \(L{i^ + }\) pénètrent en \({O_2}\) dans un champ magnétique uniforme perpendiculaire au plan du schéma et parviennent dans la zone de réception inclinée d’un angle \(\alpha \) sur la verticale (Voir Figure 2).
2.2.1. Préciser en le justifiant le sens du vecteur. 0,5pt
2.2.2. Montrer que le mouvement de chaque ion, dans le champ magnétique est circulaire uniforme de rayon: \(R = \frac{1}{B}\sqrt {\frac{{2m\left| U \right|}}{e}} \) 0,5pt
2.3. Montrer que la distance \({O_2}M\) du point d’impact a pour expression 0,5pt
2.4. Exprimer la distance d séparant les points d’impact des deux types d’ions à leur arrivée dans la zone de réception, en fonction de \(B\), \({m_2}\), \({m_2}\), \(\alpha \) et \(e\). 0,5pt
Faire l’application numérique. 0,5pt
Données : \(\left| U \right| = {10^4}V\); B = 0,2T; \({m_1} = 6u\); \({m_2} = 7u\); \(1u = 1,6 \times {10^{ - 27}}kg\); \(\alpha = {60^o}\); \(e = 1,6 \times {10^{ - 19}}C\).

Partie : B Évaluation des compétences / 16 points

Situation problème 1 / 8 points
Compétence visée : Analyser le fonctionnement d’un circuit comportant un condensateur.
Le poste radio FM de ton père ne capte plus les chaines. Le technicien diagnostique que le condensateur du circuit d’accord est défectueux et ne porte plus les inscriptions. Le circuit d‘accord, est un circuit oscillant accordable par variation de la capacité C 0 du condensateur. Il permet de sélectionner les ondes électromagnétiques souhaitées. Le schéma du circuit est donné dans le document 1.
Document 1 : schéma du circuit d’accord
Le technicien déclare que le circuit d’accord est un oscillateur harmonique.
Document 2 : autres informations - On admettra que :
L’onde électromagnétique est sinusoïdale de fréquence \({f_P}\).
• Le circuit sélectionne les fréquences \({f_P}\) pour lesquelles \({f_P} = {f_0}\) (\({f_0}\) est la fréquence propre du circuit d’accord).
• La bande de fréquences porteuses FM va de 87,5 à 108 MHz.
• L’inductance de la bobine : L = 2,00 H.
A partir de tes propres connaissances et en exploitant les informations ci – dessus :
1. Prononce-toi sur la déclaration du technicien. 4 pts
2. Aide le technicien à réparer le poste radio. 4 pts
Situation problème 2 : 8 points
Compétence visée : appliquer les lois de Newton pour résoudre un problème.
Un groupe d’élèves d’une classe scientifique se trouvant dans un laboratoire, voudrait caractériser le lieu de leur manipulation. A cet effet, leur enseignant met à leur disposition un pendule pesant constitué d’un grand cerceau de centre de centre I, de rayon R et de masse M, puis d’un petit cerceau de centre J, de rayon \(r = \frac{R}{2}\)et de masse \(m= \frac{M}{2}\)Le petit cerceau est soudé au point K du grand cerceau tel que les points O, I, J, K sont alignés. Les deux cerceaux sont solidaires et appartiennent à un même plan vertical. Le système ainsi constitué est mobile autour d’un axe fixe horizontal ( ∆ ) passant par le point O du grand cerceau.
O est diamétralement opposé à K. les élèves imposent alors au système de la figure 3 ci-dessus, des oscillations de rotation de faibles amplitudes autour de l’axe ( ∆ ). En modifiant le rayon R du grand cerceau, ils mesurent à chaque fois la durée ∆? de vingt (20) oscillations effectuées par le système. Les résultats de leur expérience sont consignés dans le tableau suivant :

A travers une démarche scientifique basée sur l’exploitation des informations fournies par ces élèves, caractérise le lieu de l’expérience. 8 pts
Donnée : Le moment d’inertie d’une circonférence pesante de masse M et de rayon R par rapport un axe passant par son centre d’inertie G est donnée par la relation : \({J_M} = M{R^2}\)
Consigne : on prendra \({\pi ^2} = 10\) et éventuellement l’échelle 1/5 suivant l’axe des abscisses et 3/1 sur l’axe des ordonnées.