I- Évaluations des Ressources : (15 points)

Exercice 1 : 4,75 points

l- Soit \(m\) un nombre impair supérieur ou égal a 9.
1) Démontrer que si \(m = 2n + 1\), \(n \in \mathbb{N}\) alors \(m = \frac{{\left( {n + 2} \right)\left( {n + 1} \right)}}{2}\) \( - \frac{{n\left( {n - 1} \right)}}{2}\) 0,5 pt
2) En déduire que :
a) Si \(n\) est pair alors \(\exists k \in \mathbb{N}\) tels que : \(m = (k + 1)(2k + 1)\) \( - k(2k - 1)\). 0,5 pt
b) Si \(n\) est impair alors \(\exists k \in \mathbb{N}\) tels que : \(m = (k + 1)(2k + 3) \) \(- k(2k + 1)\). 0,5 pt
3) a) Montrer \(m\) s’écrit sous la forme \(m = Ax – By\) avec \(x\) et \(y\) des nombres entiers de parités différentes et tels que . \(\left\{ \begin{array}{l}A - B = 1\\x - y = 2\end{array} \right.\) 0,5 pt
b) Décomposer 29 et 31 sous la forme \(Ax – By\). 0,5 pt
4) Établir un théorème que vérifie un nombre impair supérieur ou égal à 9. 0,5 pt
II-
1- Calculer pour tout entier naturel \(n\) non nul \({I_n} = \int\limits_0^1 {\frac{{{x^{n - 1}}}}{{1 + {x^n}}}} \) 0,5 Pt
2- On lance un dé cubique dont les faces sont numérotées de 1 à 6 et on note \(\Omega \) l’univers associé à cette épreuve. Soit \(\alpha \) un nombre réel, on considéré l’application :
\(P:\Omega \to \mathbb{R}\)
\(k \mapsto {k^2} \times \alpha \times {I_k}\)
Déterminer \(\alpha \) pour que \(P\) soit une probabilité sur \(\Omega \) .
3- On suppose que \(\alpha = \frac{1}{{21\ln 2}}\), Calculer la probabilité de l'événement
A « Obtenir un nombre dont l'écriture en base 2 contient au moins deux fois le chiffre 1 ›› 0,75pt;

Exercice 2 : 5,25 points

I- Une compagnie aérienne utilise huit aéroports que l’on nomme A, B, C, D, E, F, G et H.
Entre certains de ces aéroports, la compagnie propose des vols dans les deux sens.
Cette situation est représentée par le graphe \(\Gamma \) ci-dessous , dans lequel :
• Les sommets représentent les aéroports.
• Les arêtes représentent les liaisons assurées dans les deux sens par la compagnie et sont par coût de chaque vol, exprimé en milliers de FCFA.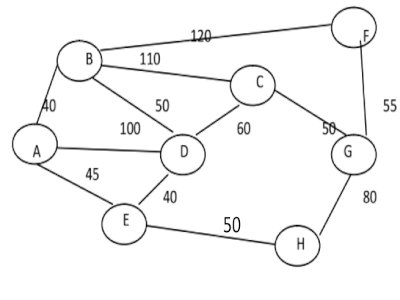
1- Déterminer en justifiant, si le graphe \(\Gamma \) est complet 0,5 pt
2- Déterminer en justifiant si le graphe \(\Gamma \) est connexe 0,5 pt
3- Un voyageur partant de l’aéroport A doit se rendre à l'aéroport G. en utilisant l’algorithme de Dijkstra, déterminer le moins cher. En déduire le coût. 1 pt

II- Le plan est muni d'un repère orthonormé \(\left( {O,i,j} \right)\). Soit \(f\) la transformation du plan qui à tout point \(M(x,y)\) associe le point \(M’(x’,y’)\) tel que : \(\left\{ \begin{array}{l}x' = x + y\sqrt 3 \\x' = - x\sqrt 3 + y\end{array} \right.\) et \(\left( \varepsilon \right)\) la courbe d'équation : \(7{x^2} + 13{y^2} + \) \(6\sqrt 3 xy = 4\)
a) Montrer que \(f\) est une similitude directe plane dont on déterminera les éléments caractéristiques de \(f\). 0,75 pt
b) Démontrer qu’une équation de \(\left( {\varepsilon '} \right)\)image de \(\left( \varepsilon \right)\) par \(f\) est \(4{x^2} + {y^2} = 4\). 0,75 pt
c) Déterminer la nature et les éléments caractéristiques de \(\left( {\varepsilon '} \right)\) puis celle de \(\left( \varepsilon \right)\) (foyers, sommets et excentricité) 0 75 pt
d) Construire dans le même repéré \(\left( {\varepsilon '} \right)\)et \(\left( \varepsilon \right)\).

Exercice 3 : 5 points

I- Le plan muni d’un repère orthonormé (O,I,J). Soit \(f\) la fonction numérique à variable définie sur \(\left] {0; + \infty } \right[\) par \(f(x) = \frac{1}{{1 + x}} - \) \(\ln (1 + x) + \ln x\) et \((C)\) sa courbe représentative dans le repère (on prendra pour unité graphique 2 cm sur chaque axe).
On désigne par \({\left( {{U_n}} \right)_{n \succ 0}}\) la suite de terme général : \({U_n} = - \ln x + \sum\nolimits_{k = 1}^n {\frac{1}{k}} .S\)
1) a) Déterminer les limites de la fonction \(f\) à droite en 0 et \( + \infty \) 0,5 pt
2) a) Montrer que pour tout réel \(x \in \left] {0; + \infty } \right[\), on a \(f'(x) = \frac{1}{{x{{\left( {x + 1} \right)}^2}}}\)
c) Dresser sur \(\mathbb{R}\) le tableau de variation de la fonction \(f\). 0,25 pt;
2) a) Montrer que \(f\) est une bijection de \(x \in \left] {0; + \infty } \right[\) vers \(\left] { - \infty ;0} \right[\). 0,25 pt
b) Construire dans le même repère la courbe \((C)\) et \((C')\), courbe de \({f^{ - 1}}\).
c) On désigne par \(\alpha \) un réel strictement positif et inférieur à 1.
On note \(D = \{ M(x,y)\backslash \alpha \) \( \le x \le 1;f(x) \le y \le 0\} \), En utilisant une intégration par partie montrer que l'aire du domaine \(D\) en cm2 est \(aire(D) = 4[\ln 2 - \) \(\alpha \ln \left( {\frac{{\alpha + 1}}{\alpha }} \right)]\) cm².
d) Calculer la limite de l’aire quand \(\alpha \) tend vers 0 0,25 Pt

ll- L'espace \(\xi \) est muni du repère orthonormé direct \(\left( {O;\overrightarrow i ,\overrightarrow j ,\overrightarrow k } \right)\). \(f:M\left( \begin{array}{l}x\\y\\z\end{array} \right) \in \xi \mapsto \) \(M'\left( \begin{array}{l}x'\\y'\\z'\end{array} \right) \in \xi \) tel que : \(\left\{ \begin{array}{l}x' = \frac{1}{3}\left( { - x - 2y - 2z + 6} \right)\\y' = \frac{1}{3}\left( { - 2x - y + 2z - 6} \right)\\z' = \frac{1}{3}\left( { - 2x + 2y - z + 12} \right)\end{array} \right.\)
1- Démontrer que \(f\) est un demi-tour dont on précisera l’axe \((D)\). 0,5 pt
2- Soit \(B(0,0.3)\) et \(C(-1 ;0 ;1)\), vérifier que \(B \in \left( D \right)\) et que \(C \notin \left( D \right)\). 0.5 Pt
3- Soit \((P)\) le plan de \((ABC)\) et \((P')\) le plan contenant \((D)\) et perpendiculaire à \((P)\)
a) Trouver une équation de \((P)\) et une équation de \((P’)\) 0,5 pt
b) Justifier que \(f = {S_{(P)}} \circ {S_{(P')}}\) 0,5 pt
4- Soit \(H\) le projeté orthogonal de \(C\) sur \((D)\) et \(\left( \pi \right)\) le plan parallèle à \((P')\) passant par \(C\).
a) Trouver les coordonnées de H. 0 5 Pt
b) Déterminer \({S_{(P)}} \circ {S_{(P')}}\) 0,25 pt

II- Évaluations des compétences : (5 points)

Situation
Dans le cadre de la promotion du tourisme, la communauté de Yaoundé a entrepris la réfection d’une route et la construction d’un musé d'architecture moderne.
La route est modélisable par une portion de la courbe \(\left( \Gamma \right)\) de la fonction numérique \(f\) de la variable réelle \(x \in \left[ {\frac{1}{2};2} \right]\) par \(f(x) = \frac{{{x^2}}}{4} - \frac{{\ln x}}{2}\). L’unité de longueur étant le kilomètre (km), on admet que la longueur de cette route est \(I = \int_{\frac{1}{2}}^2 {\sqrt {1 + {{\left[ {f'(x)} \right]}^2}} dx} \)
On estime qua 10 mètres de réfection de cette route coûtera 300000 FCFA.
Le musé d’architecture moderne sera réalisée sur un terrain rectangulaire dont les dimensions en mètre sont deux entiers naturel \(a\) et \(b\) vérifiant \(\left\{ \begin{array}{l}a - b = 22932\\ppcm(a,b) = 98280\end{array} \right.\) L’unité de longueur est le mètre.
Un espace vert ayant la forme d'un losange ABCD doit y être aménagé. Les points A, B, C et D étant les sommets de l’ellipse dont une équation est \(2{x^2} + 3{y^2} - \) \(12x + 9y + 24 = 0\).L'unité de longueur étant le kilomètre. Dans cet espace, on y sèmera du gazon sur toute la superficie. On estime a 35000 FCFA le prix d'un mètre-carré de ce gazon.

Tâches
1- Estimer la dépense à opérer pour refaire entièrement la route. 1,5 pt
2- Déterminer les dimensions du terrain devant abriter le musé architectural. 1,5 pt
3- Estimer la dépense pour l’achat du gazon qui doit recouvrir entièrement l’espace vert. 1,5 pt
Présentation : 0,5 pt