L’épreuve comporte deux parties A et B étalées sur deux pages.
Partie A : Évaluation des ressources 14,5 pts
Exercice 1 (5 points)
A. On considère dans R3 le système suivant : {40x+35y+25z=175550x+30y+20z=171070x+40y+50z=2820.
Un seul triplet parmi les triplets (?,?,?) suivants est la solution de ce système. Écrire le triplet correspondant à la bonne réponse sur ta feuille de composition. 1pt
a) (15; 13; 28),
b) (15; 23; 14),
c) (15; 18; 21).
B. Trois groupes de personnes d’un village se réunissent pour acheter du sable, du gravillon et du ciment en vue de construire une école. Le tableau ci-dessous donne la contribution de chaque membre par type de matériau de construction en fonction de son groupe.
Type de matériau Contribution par membre
| Type de matériau | Contribution par membre | ||
| Groupe A |
Groupe B | Groupe C | |
| Sable |
4000 | 3500 |
2500 |
| Gravillon | 5000 | 3000 | 2000 |
| Ciment |
7000 | 4000 | 5000 |
Le sable, le gravillon et le ciment nécessaires à la construction coûtent en FCFA respectivement : 175 500, 171 000 et 282 000.
a) Calculer le nombre de membres de chaque groupe. 1,5pt
b) Quel est le montant des contributions du groupe B ? 0,5pt
C. On procède à une nouvelle répartition par tranche d’âge des membres des trois groupes et on obtient le tableau suivant :
| Tranche d’âge | [25; 30[ |
[30; 35[ | [35; 40[ | [40; 45[ |
[45; 50[ |
| Effectif |
8 |
12 |
15 | 10 |
9 |
a) Donner la classe modale de cette série statistique. 0,25pt
b) Calculer la moyenne de cette série statistique. 0,75pt
D. Dans la répartition ci-dessus, le tiers des membres est constitué des femmes. On choisit au hasard et simultanément trois membres chargés de superviser les travaux.
a) Déterminer le nombre de choix possibles. 0,5pt
b) Déterminer le nombre de choix comportant une femme et deux hommes. 0,5pt
Exercice 2 (3 points)
1) Résoudre dans R l’équation : 2t2+√2t−2=0.0,5pt
2) Montrer que : −√3cosx+sinx= 2cos(x−5π6) 1pt
3) a) Utiliser les résultats des questions 1) et 2) pour résoudre dans ]−π,π] l’équation 1pt
E:(2cos2x+√2cosx−2) (−√3cosx+sinx−1)=0
b) Représenter les images des solutions de (?) sur le cercle trigonométrique. 0,5pt
Exercice 3 (3,75 points)
EFG est un triangle rectangle isocèle en E, I désigne le milieu de l’hypoténuse. On donne en centimètres EF=4.
1) a) Déterminer et construire le barycentre H du système :
{(E;1),(F;−1),(G;−1)} 0,75pt
b) Démontrer que le quadrilatère EFHG est un carré. 0,5pt
2) a) Déterminer l’ensemble (Γ) des points M du plan tels que : MF2+MG2=24. 0,75pt
b) Tracer (Γ). 0,25pt
3) On considère l’homothétie ℎ de centre E et de rapport 32. Les points F’, G’ et H’ désignent les images respectives des points F, G et H par ℎ.
a) Construire les points F’, G’ et H’. 0,75pt
b) Déterminer la nature du quadrilatère EF’H’G’. 0,25pt
c) Déterminer l’image de (Γ) par ℎ. 0,5pt
Exercice 4 (3,25 points)
Soit ? et ? les fonctions numériques de la variable réelle ? définies par : f(x)=x+1x et g(x)=x+1x−1. On désigne par (??) et (??) les courbes représentatives respectives des fonctions ? et ? dans le plan muni d’un repère orthonormé.
1) Justifier que l’ensemble de définition ?? de la fonction ? est ]−∞,0[∪]0,+∞[. 0,25pt
2) Déterminer les limites de ? aux bornes de ? ? et en déduire une asymptote verticale à la courbe (?? ) . 1,25pt
3) Montrer que la droite (?) d’équation ?=? est une asymptote oblique à la courbe (??). 0,5pt
4) a) Montrer que tout x≠1, g(x)=f(x−1)+1. 0,5pt
b) En déduire que (??) est l’image de (??) par une transformation du plan dont on donnera la nature et l’élément caractéristique. 0,75pt
Partie B : Évaluation des compétences (5 points)
Situation
Le 1 er janvier 2023, la population d’une petite ville du Cameroun est de 40 000 habitants.
Cette population augmente de 5% chaque année par les naissances et reçoit aussi par an 1000 immigrants suite à l’exode rural. La population scolaire de cette ville représente 25% des habitants et qu’il faut un enseignant pour 40 élèves.
Ben est un habitant de cette ville et dispose d’un terrain limitrophe à un mur d’une construction qu’il utilise pour clore une parcelle rectangulaire de son terrain. Il dispose de 100 m de grillage pour cette clôture. 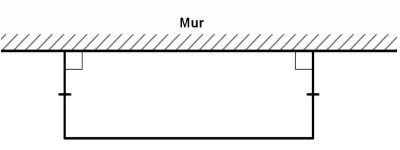
Tâches
1) Déterminer le nombre d’enseignants de cette ville en 2023. 1,5pt
2) Déterminer la population de cette ville le 1 er janvier 2025. 1,5pt
3) Déterminer la plus grande superficie que M. Ben peut clôturer. 1,5pt
Présentation : 0,5pt


