Partie A : Évaluation des ressources (10pts)
I- Activités numériques / 5 pts
Exercice 1 : / 1 ,5pt
1- Calculer le nombre \(A = \frac{3}{3} \times \frac{6}{5} + \left( {\frac{2}{3} + \frac{6}{5}} \right)\) et donner le résultat sous la forme d’une fraction irréductible. 0,5pt
2- On donne \(B = \frac{2}{{2 - \sqrt 3 }}\)
a) Écrire le nombre \(B\) sans radical au dénominateur. 0,5pt
b) Sachant que \(1,732 \prec \sqrt 3 \prec 1,733\). Donner un encadrement d’ordre 2 de \(4 + 2\sqrt 3 \) 0,5pt
Exercice 2 : 1,5pt
1- On considère l’impression littérale \(E = {\left( {2x - 6} \right)^2} - 36\) 0,5pt
a- Factorise \(E\)
b- Résoudre dans \(\mathbb{R}\) l’équation : \(\left( {2x - 9} \right)\left( {2x + 4} \right) = 0\) 0,5pt
2- Répondre par vraie ou faux
a) L’inéquation \( - 3x + 2 \ge x - 5\) a pour ensemble solution \(S = \left[ {\frac{7}{4}; \to } \right[\) 0,25pt
b) L’inéquation \(8x - 9 \le 15x - 12\) a pour ensemble solution \(S = \left] { \leftarrow ;\frac{3}{7}} \right]\) 0,25pt
Exercice 3 : 2 pts
Le tableau statistique ci-dessous est celui des notes en mathématiques de 50 élèves d’une classe de troisième. Ces notes sont regroupées en classes d’amplitude 5.
| Notes | [0 ; 5 [ | [5 ; 10 [ | [10 ; 15[ | [15;20 [ | Total |
| Effectifs | 17 | 12 | 10 | 50 | |
| Centre des classes | 2,5 | 12,5 | / |
1- Reproduire et compléter le tableau ci-dessus. 0,75pt
2- Donner la classe modale de cette série statistique. 0,25pt
3- Choisir et recopier la bonne réponse parmi celles qui sont proposées. La moyenne des notes en mathématiques de cette classe est : 1 pt
a) 8 ;
b) 8,5
c) 9
d) 9,5
II- Activités géométriques / 5 pts
Exercice 1 : / 1,5pt
Soit ABC un triangle rectangle en A avec AB= 4 cm et BC = 6 cm
1- Montrer que \(AC = 2\sqrt 5 \) cm 0,5pt
2- On fait tourner ce triangle autour de l’axe \((AB)\).
Quel solide de révolution obtient –on? Calculer son volume . 1pt
Exercice 2 : / 1,5pt
L’unité de longueur est le centimètre. Dans un repère orthonormé \((O, I, J)\) du plan, on donne les points \(A(3,2)\), \(B (-1 ; 3)\) et \(C(2 ;-2)\)
1- Calculer les coordonnées des vecteurs \(\overrightarrow {AB} \)et \(\overrightarrow {AC} \) 0,5pt
2- Justifier que les vecteurs \(\overrightarrow {AB} \) et \(\overrightarrow {AC} \) sont orthogonaux. 0,5pt
3- Écrire une équation cartésienne de la droite \((AB)\). 0,75pt
Exercice 3 : / 2 pts
L’unité de longueur est le mètre. La figure ci-dessous représente une partie de la charpente du toit d’une maison. 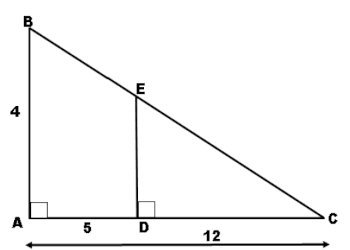 \(ABC\) est un triangle rectangle en \(A\) tel que \(AB= 4\) et \(AC =12\). \(D\) est le point du segment \([AC]\) tel que \(AD=5\). La droite passant par \(D\) et perpendiculaire à \((AC)\) coupe la droite \((BC)\) en E
\(ABC\) est un triangle rectangle en \(A\) tel que \(AB= 4\) et \(AC =12\). \(D\) est le point du segment \([AC]\) tel que \(AD=5\). La droite passant par \(D\) et perpendiculaire à \((AC)\) coupe la droite \((BC)\) en E
1- Calculer la longueur \(BC\) 0,5 pt
2- Calculer la longueur ED 0,5 pt
3-a Calculer \(\tan \widehat {ABC}\)
b- En déduire la mesure en degré de l’angle
Partie B : Évaluation des compétences / 10 pts
Situation
SAWALDA dispose d’une parcelle de terrain qu’il a divisé pour servir de jardin. Sur une partie ayant la forme d’un demi-cercle de diamètre \([AB]\), il veut cultiver de la tomate et sur autre partie triangulaire veut cultiver de l’oignon. Il souhaite utiliser 10 plantes de tomates pour 3m2 et 25 plantes d’oignons pour 1m2.
Pour arroser son jardin, il utilise une réserve d’eau d’un château ayant la forme d’un cylindre de diamètre 1,5m et de hauteur 3m pour arroser suffisamment son jardin. Il doit utiliser 1000L d’eau.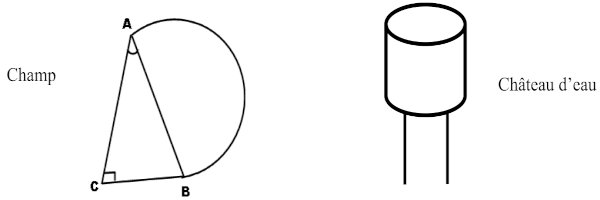 On donne \(AC = 10\sqrt 3 \) \(mes\widehat {BAC} = {30^o}\), \(\widehat {ACB} = {90^o}\)
On donne \(AC = 10\sqrt 3 \) \(mes\widehat {BAC} = {30^o}\), \(\widehat {ACB} = {90^o}\)
On prendra \(\sqrt 3 = 1,73\) et \(\pi = 3,14\)
Tâches :
1- Combien de fois SAWALDA pourra-t-il arroser son jardin avec son château plein ? 3 pts
2- Combien de plantes de tomates doit-il utiliser pour occuper entièrement la surface réservée à la culture des tomates ? 3 pts
3- Combien de plantes d’oignons doit-il utiliser pour occuper entièrement la surface réservée à la culture des oignons ? 3 pts
Présentation 1 pt


