Partie A : Évaluation des ressources : 15 points

EXERCICE 1 : 4,5 points

I/ (Série C uniquement)

On considère dans \(\mathbb{R}\) le polynôme \(P\) défini par :
\(P(x) = {x^4} - 32{x^3} + \) \(186{x^2} - 280x + 125\)
1. Montrer que tout entier relatif \(𝑛\) solution de l’équation \(P(𝑥) = 0\) divise 125. 0,5pt
2. Résoudre dans \(\mathbb{R}\) l’équation \(P(𝑥) = 0\) . 1pt

I/ (Série E uniquement)

1. Résoudre dans \(\mathbb{C}\) l’équation \(1 + z + {z^2} + ...\) \( + {z^6} = 0\) 0,75pt
2. Calculer la valeur exacte de \(\cos \frac{{2\pi }}{7} + \cos \frac{{4\pi }}{7} + \cos \frac{{6\pi }}{7}\). 0.75pt

II/ Une urne contient quatre boules noires et deux boules blanches. Soit \( 𝑛\) un entier naturel supérieur ou égal à 2. On répète \(𝑛\) fois l’épreuve qui consiste à tirer une boule de l’urne, puis à la remettre dans l’urne ; on suppose que toutes les boules ont la même probabilité d’être tirées et que les tirages sont indépendants. On note \({p_n}\)la probabilité de tirer exactement une boule blanche lors des \(𝑛 – 1\) premiers tirages et une boule blanche lors du \({n^{ième}}\) tirage.
1. Calculer les probabilités \({p_2}\) et \({p_3}\). 0,5pt
2. On considère les évènements suivants :
\({B_n}\) : « Tirer une boule blanche lors du \({n^{ième}}\) tirage » ;
\({U_n}\) : « On tire une boule blanche et une seule lors des \(𝑛 − 1\) premiers tirages».
a) Calculer la probabilité de l’évènement \({B_n}\). 0,5pt
b) Exprimer la probabilité de l’évènement \({U_n}\) en fonction de \(𝑛\) . 0,5pt
c) En déduire l’expression de \({p_n}\)en fonction de \(𝑛\) et vérifier que : \({p_n} = \frac{{n - 1}}{4} \times {\left( {\frac{2}{3}} \right)^n}\) 0,5pt
3. On pose : \({S_n} = {p_2} + {p_3} + ... + {p_n}\).
a) Démontrer par récurrence que pour tout entier naturel \(𝑛\) supérieur ou égal à 2, on a : \({S_n} = 1 - \left( {\frac{n}{2} + 1} \right) \times {\left( {\frac{2}{3}} \right)^n}\) 0,75pt
b) Déterminer la limite de la suite (\({S_n}\)) . 0,25pt

EXERCICE 2 : 4 points

L’espace est muni d’un repère orthonormé direct \(\left( {O;\overrightarrow i ,\overrightarrow j ,\overrightarrow k } \right)\). On considère les points \(A(1 ; 1 ; 1)\) , \(B(2 ; 0 ; 1)\) , \(C(3 ; −2 ; −2)\) et \(D(1 ; 0 ; −3)\).
1. a) Montrer que les points A, B et C sont non alignés, puis déterminer une équation
cartésienne du plan \( (ABC)\) . 0,5pt
b) Justifier que \(D\) n’appartient pas au plan \((ABC)\) , puis calculer le volume du tétraèdre \(ABCD\) . 0,75pt
2. On considère le plan \((𝑃)\) d’équation \(3𝑥 + 3𝑦 − 𝑧 − 5 = 0\) .
Déterminer l’expression analytique de la réflexion de plan \((𝑃)\) . 0,75pt
3. Dans l’ensemble \(𝑊\) des vecteurs de l’espace, on considère l’endomorphisme \(\varphi \) défini par : \(\varphi (\overrightarrow i ) = \overrightarrow i \), \(\varphi (\overrightarrow j ) = - 2\overrightarrow j + \overrightarrow k \)et \(\varphi (\overrightarrow k ) = 4\overrightarrow j - 2\overrightarrow k \).
a) Déterminer la matrice \(M\) de \(\varphi \) dans la base \(B = \left( {\overrightarrow i ,\overrightarrow j ,\overrightarrow k } \right)\). 0,25pt
b) Déterminer le noyau de \(\varphi \) et préciser une base. 0,5pt
c) Déterminer l’image de \(\varphi \) et préciser une base. 0,5pt
d) Soit \(B' = \left( {\overrightarrow i ,\overrightarrow u ,\overrightarrow v } \right)\) où \(\overrightarrow u = 2\overrightarrow j + \overrightarrow k \) et \(\overrightarrow v = - 2\overrightarrow j + \overrightarrow k \).
Montrer que \(𝐵′\) est une base de \(𝑊\) et déterminer la matrice \(M′\) de \(\varphi \) dans la base \(𝐵′\) . 0,75pt

EXERCICE 3 : 3,5 points

Soit la fonction numérique \(𝑓\) définie par : \(f(x) = \int\limits_1^x {\frac{{\ln t}}{{\sqrt {1 + {t^4}} }}} dt\). On désigne par \((𝐶)\) sa courbe représentative dans un repère orthonormé \((O;\overrightarrow i ,\overrightarrow j )\).
1. a) Justifier que \(𝑓\) est définie sur \(\left] {0; + \infty } \right[\). 0,25pt
b) Calculer \(𝑓′(𝑥)\) et en déduire le sens de variation de \(𝑓\) . 0,5pt
2. a) Pour tout réel \(x \succ 0\), calculer à l’aide d’une intégration par parties \(f(x) = \int\limits_1^x {\frac{{\ln t}}{{{t^2}}}} dt\) 0,5pt
b) Montrer que pour tout réel \(x \succ 0\): \(\frac{1}{{\sqrt 2 }}\left( {1 - \frac{1}{x} - \frac{{\ln x}}{x}} \right)\) \( \le f(x) \le \) \(\left( {1 - \frac{1}{x} - \frac{{\ln x}}{x}} \right)\) et en déduire
un encadrement de la limite de \(𝑓\) en \({ + \infty }\). 0,75pt
3. Soit \(𝑔\) la fonction définie sur \(\left] {0; + \infty } \right[\) par : \(g(x) = f(x) + f\left( {\frac{1}{x}} \right)\)
a) Démontrer, en calculant \(𝑔′(𝑥)\) , que \( 𝑔 \) est la fonction nulle sur \(\left] {0; + \infty } \right[\). 0,5pt
b) En déduire un encadrement de la limite de \(𝑓\) en 0. 0,25pt
c) Tracer l’allure de la courbe \((𝐶)\) . 0,75pt

EXERCICE 4 : 3 points

Le plan est muni d’un repère orthonormé direct \((O;\overrightarrow i ,\overrightarrow j )\). On considère une courbe \((𝐻 )\) d’équation \({x^2} - 4{y^2} - 2x - 3 = 0\).
1. Montrer que \((𝐻 )\) est une hyperbole dont on déterminera les sommets. 0,75pt
2. a) Vérifier que le point \(A\left( {1 + 2\sqrt 2 ;1} \right)\) appartient à \((𝐻 )\) . 0,25pt
b) Déterminer une équation de la tangente \((𝑇)\) à \((𝐻 )\) en \(A\). 0,5pt
3. Soit \(\theta \) un réel de l’intervalle \(\left] {0;\frac{\pi }{4}} \right[\). On considère dans \(\mathbb{C}\) l’équation
\(\left( {{E_\theta }} \right):\left( {{{\cos }^2}\theta } \right){z^2} - 2\) \(\left( {{{\cos }^2}\theta + 2\cos \theta } \right)z + 5 + \) \(4\cos \theta = 0\)
a) Résoudre l’équation \(\left( {{E_\theta }} \right)\). 1pt
b) Soient \({M_1}\) et \({M_2}\) les images respectives des solutions \({z_1}\) et \({z_2}\) .
Montrer que \({M_1}\) et \({M_2}\) varient sur une branche \((𝐵)\) de l’hyperbole \((𝐻 )\) . 0,5pt

PARTIE B : ÉVALUATION DES COMPÉTENCES : 5 points

Situation :
En 2000, la population d’une ville était de 4,75 millions d’habitants et de 5,5 millions d’habitants en 2005. La vitesse d’accroissement de la population est proportionnelle au nombre d’habitants. Les autorités de la ville voudraient savoir en quelle année cette population aura atteint 10 millions d’habitants.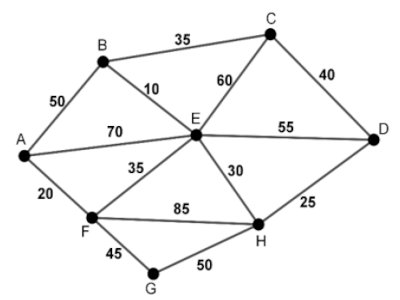
Sur le graphe ci-dessus, les lettres représentent certains quartiers de cette ville et les nombres représentent en hm, la distance à parcourir sur une route qui relie un quartier à un autre lorsqu’elle existe. Une société d’électricité voudrait implanter la lumière dans chaque quartier de cette ville en partant d’un quartier choisi au hasard et en utilisant le moins de câble possible. Le responsable des travaux doit quitter de la base du chantier installée au quartier A pour le quartier H où il a une séance de travail avec le maire de la ville. Compte tenu des impératifs, il doit emprunter le plus court chemin possible.

Tâches :
1. Proposer un itinéraire à ce responsable des travaux. 1,5pt
2. Quelle est la longueur minimale du câble à utiliser pour cette implantation ? 1,5pt
3. En quelle année cette population atteindra 10 millions d’habitants ? 1,5pt
Présentation : 0,5pt