Partie A : Évaluation des ressources : 15 points

Exercice 1 : 5 points

Pour chacune des questions suivantes, trois réponses sont proposées parmi lesquelles une seule est correcte.
Recopier le numéro de la question suivi de la lettre qui correspond à la réponse correcte.
1) Soit le polynôme \(P(x) = 2{x^2} + 4x - 2\). Sa forme canonique est : 1pt
a) \(2\left[ {{{\left( {x + 2} \right)}^2} - 1} \right]\);
b) \(2\left[ {{{\left( {x - 2} \right)}^2} - 2} \right]\);
c) \(2\left[ {{{\left( {x + 1} \right)}^2} - 2} \right]\).
2) Le nombre de possibilité d’effectuer un tirage successif sans remise de 03 boules dans une urne de 05 boules est. 1pt
a) \(A_5^3\);
b) \(C_5^3\);
c) \(C_3^5\).
3) L’inéquation \({x^2} - x - 6 \prec 0\) à pour solution :
a) \(\left[ { - 2;6} \right]\);
b) \(\left] { - 2;3} \right[\);
c) \(\left] { 2;3} \right[\). 1pt
4) L’ensemble solution de l’équation \(\frac{{3x + 3}}{{x - 1}} = \frac{4}{x}\) est :
a) \(\left\{ { - 1;\frac{3}{2}} \right\}\) ;
b) \(\emptyset \) ;
c) aucune solution. 1pt
5) Le système \(\left\{ \begin{array}{l}3x - y = 1\\ - 2x + 5y = 8\end{array} \right.\) a pour couple solution :
a) \((𝟏 ;𝟏 )\) ;
b) \((𝟐 ;𝟏 )\) ;
c) \((𝟏 ;𝟐 ) \). 1pt

Exercice 2 : 6 points

La courbe \(\left( \Gamma \right)\) ci-dessous est celle d’une fonction \(𝑓\) définie sur un intervalle de \(\m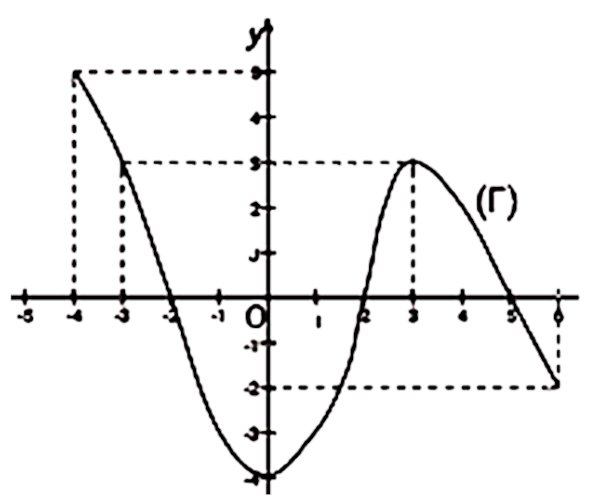athbb{R}\) .
1) Donner l’ensemble de définition de \(𝑓\) . 0.5 pt
2) Déterminer les images par \(𝑓\) de 0 et 6 . 1 pt
3) Déterminer les antécédents par \(𝑓\) de 3 et − 4 . 0.75 pt
4) Déterminer l’image directe de \(\left[ { - 4;0} \right]\). 0.75 pt
5) Dresser le tableau de signe de \( 𝑓\) . 1 pt
6) Dresser le tableau de variation de \(𝑓\) . 1 pt
7) Résoudre graphiquement l’équation et l’inéquation:
a) \(f(x) = 0\);
b) \(f(x) \le 3\). 1 pt

Exercice 3 : 4 points

Une étude porte sur le nombre d’enfants scolarisés par famille dans une ville de l’Extrême-Nord. On obtient la série statistique suivante :

1) Construire le diagramme en bâtons de la série statistique. 1pt
2) Dresser le tableau des effectifs cumulés croissants et décroissants. 1pt
3) Déterminer le mode, la médiane et la moyenne de cette série. 1pt
4) Calculer l’écart type. 1 pt

Partie B : Évaluation des compétences : 4,5 points

Désireux d’avoir une meilleure condition de vie tant pour eux que pour leurs enfants, un groupe de 04 enseignants décident d’explorer le secteur de l’élevage. Ils se disent alors qu’il leur faut un local de forme rectangulaire de superficie 1600 m 2 et de clôture 89 m. Après étude du devis, il leur faut 3 000 000 FCFA qu’ils réunissent après deux années de cotisations. Ils prévoient 498 000 FCFA pour l’achat des poules et de moutons et 300 000 FCFA pour l’alimentation. Lors de l’achat il leur est dit qu’une poule coûte 2 400 FCFA et un mouton 30 000 FCFA et ils s’accordent de prendre 35 animaux en tout espérant revendre pendant les fêtes une poule à 3 500 FCFA et un mouton à 55 000FCFA. Pour le suivi et le gardiennage, ils recrutent, dans le village de l’un d’eux, M. Ahmadou qui, étant venu en hâte en ville n’a pas emporté des vêtements. Ils lui offrirent 03 pantalons, 02 paires de chaussures et 04 chemises. Sachant que pour se vêtir il faut un pantalon, une chemise et une paire de chaussure.
1) Déterminer les dimensions du terrain. 1,5 pt
2) Dans le cas où ils vendent tous les animaux achetés, réaliseront-ils un bénéfice ? 1,5 pt
3) Combien de façons différentes M Ahmadou pourra-t-il se vêtir. 1,5 pt
Présentation : 0,5 pt