Partie I : Évaluation des ressources / 24 points

Exercice 1 : Vérification des savoirs/ 8 points

1. Définir : capteur, grandeur sinusoïdale. 2 pt
2. Donner deux applications de la radioactivité. 1pt
3. Énoncer la loi de |'attraction universelle. 2 pt
4. Répondre par vrai ou faux : 1pt
4.1 L'angle d’inclinaison d'une route dans un virage pour éviter le dérapage du véhicule dépend, de la vitesse \(V\) de celui-ci et du rayon de courbure \(r\) du virage.
4.2 Un atome n'absorbe que les radiations de fréquences égales à celles qu'il peut lui-même émettre
5. Donner l’expression de la force de Laplace et préciser les unités des différentes grandeurs physiques qui y interviennent. 2 pt

Exercice 2 : Application des savoirs/ 8 points

A. Effet photoélectrique/ 2 points

Un laser He-Ne de longueur d'onde \(\lambda \) éclaire la cathode d'une cellule photoémissive constituée d'une plaque dont le travail d’extraction est \({W_0} = 2,90 \times {10^{ - 19}}J\).
Déterminer:
1. L’énergie cinétique maximale d'un électron émis. 1 pt
2. le potentiel d'arrêt de la cellule sachant que \({E_{{C_{\max }}}} = 8,00 \times {10^{ - 20}}J\) 1pt
On donne; \(h = 6,62 \times {10^{ - 34}}J\); \(C = 3 \times {10^8}m/s\); \(e = 1,6 \times {10^{ - 19}}C\); \(\lambda = 532 \times {10^{ - 9}}m\).

B. Condensateur/ 2 points

Un condensateur de capacité \(C = 47 \times {10^{ - 6}}F\) est chargé à travers une résistance R sous une tension \(U = 200 V\).
1. Exprimer l'énergie emmagasinée parle condensateur au cours de sa charge en fonction de sa charge q et de la tension \(U\) à ses bornes 1 pt
2. Déterminer l’énergie emmagasinée parle condensateur lorsque la charge est terminée. 1 pt

C. Mouvement rectiligne sinusoïdal / 4 points

Un point matériel de masse \(m = 1\) kg accroché à un ressort, est animé d'un mouvement rectiligne sinusoïdal d'amplitude \(a = 24\) cm et de période \(T = 4\) s.
Déterminer:
1. la constante de raideur \(k\) du ressort. 2pt
2. L’élongation à la date \(t = 2\) s sachant que \(x = 24\sin \frac{\pi }{2}(t + 1)\) cm. 2 pt

Exercice 3 : Utilisation des savoirs / 8 points

A. Réactions nucléaires / 4 points

1. Soit une réaction nucléaire : \({}_3^6Li \to {}_1^2H + {}_2^4He\)
Données: La masse de \({}_3^6Li\) est 6,01512 u; celle de \({}_1^2H\) est 2,01410 u et celle de \({}_2^4He\) est 4,002s0 0 ; unité de masse atomique 1u = 931,5 Mev/ C².
1.1 Calculer la variation de l'énergie au cours de cette réaction. 2 pt
1.2 En déduire si cette réaction est spontanée. 0,5 pt
2. La transformation de l’hydrogène en hélium 4.
2.1 Écrire l’équation-bilan de la réaction nucléaire des noyaux d'hydrogène \({}_1^1H\) produisant une particule \(\alpha \) et deux positons. 1 pt
2.2 Indiquer la nature de cette réaction nucléaire provoquée. 0,5pt

B. Accélération et déflexion d'un électron dans un champ électrique / 4 points

On étudie le mouvement d'un électron émis sans vitesse initiale du point O (figure ci-dessous) ;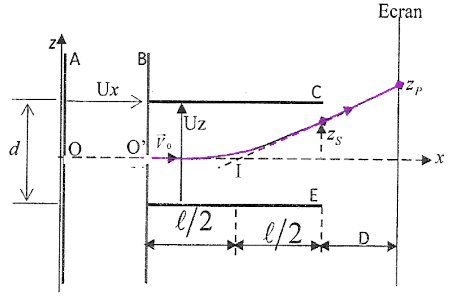
L’électron est accéléré sous l'effet d'un champ électrique uniforme entre O et O'.
Soit la vitesse \(\overrightarrow {{V_0}} \), acquise à la sortie du premier condensateur, la particule entre dans une seconde zone ou règne un champ électrique perpendiculaire au premier.
charge de L’électron \(q = - e\) et sa masse \(m\). ,
1. Déterminer les signes des tensions \({U_x}\) et \({U_z}\) entre les plaques pour que l’électron soit accéléré parla première paire de plaques, et soit dévié vers les \(z\) supérieurs à zéro par la seconde paire de plaques. 1 pt
2. Exprimer la vitesse \({V_0}\) en fonction (\(e\), \({U_x}\) et \(m\)) de l'électron à la sortie du premier condensateur. 1 pt
3. On s'intéresse au mouvement de l'électron dans le deuxième condensateur.
Exprimer l’'ordonnée \({Z_p}\) du point d'impact de l'électron sur l'écran en fonction de \(D\), \(l\)\({U_x}\), \({U_z}\) et \(d\). On rappelle que \(O'I = \frac{l}{2}\) et \(z = \frac{{{U_z}}}{{4d{U_x}}}{x^2}\)

Partie Il : Évaluation des compétences / 16 points

Situation problème 1/ 8 points

Dans le laboratoire du collège, les élèves de terminale réalisent une expérience. Ils montent un oscillateur (RLC) électrique libre (circuit 1) et constatent qu'il est le siège des oscillations, amorties (graphe 1).
Ils décident donc d’améliorer le circuit 1 et obtiennent le circuit 2 (résonance d’intensité) qui est un oscillateur électrique forcé sans amortissement (Graphe 2).
Pour expliquer le phénomène d'amortissement, NGANDO I'un des élèves estime que celui-ci est dû à la dissipation de l'énergie par effet Joule ce qui se traduit par (\(\frac{{d{E_T}}}{{dt}} = - R{i^2}\)) où \({{E_T}}\) est l’énergie totale du circuit (document 1).
Par ailleurs, les élèves ont des difficultés à choisir le GBF approprié à partir des GBF mis à leur disposition ( Document 2) pour obtenir un oscillateur non amorti.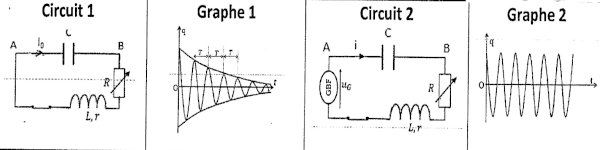
Document 1 : informations utiles V
I - Énergie totale d'un circuit RLC : \({E_T} = {E_{condensateur}} + {E_{bobime}}\)
Rappel mathématique \(\frac{{d\left( {{x^2}} \right)}}{{dt}} = 2x\frac{{dx}}{{dt}}\)
Document 2 : Caractéristiques des GBF disponibles
A : \(u = 105\sin \left( {100\pi t} \right)\)
B : \(u = 105\sin \left( {200\pi t} \right)\)
C : \(u = 105\sin \left( {100\pi t + \frac{\pi }{2}} \right)\)
D : \(u = 105\sin \left( {100\pi t} \right)\)
Données :
\(R = 295\Omega \), \(r = 5\Omega \) et \(i = 0,35\sin \left( {100\pi t} \right)\)
En exploitant les informations ci-dessus et à I'aide d'une démarche scientifique,
1. Examine la déclaration de NGANDO. 4pt
2. Aide les élèves à choisir le GBF. 4pt

Situation problème 2 / B points

Un vendeur voudrait faire la commande de plusieurs lampes pouvant éclairer de manière continue (mode normal) et de manière intermittente (mode stroboscopie). Avant de valider la commande, il a demandé deux échantillons de lampes qu'il a confiées aux élèves de terminale pour vérifier les caractéristiques indiquées sur la plaque signalétique (document 1).
Une fois au laboratoire de l’établissement les élèves réalisent les expériences suivantes :
Expérience 1
Ils observent en mode stroboscopique la surface de l'eau sur laquelle un vibreur provoque les perturbations.
Un dispositif approprié a permis de déterminer la célérité \(c\) de la vibration dans l'eau.
Dans cet éclairage, ils observent des rides circulaires immobiles concentriques. La mesure de la distance entre la 1ère et la 21e ride a donné une distance d.
Expérience 2
En éclairage continu (mode normal), Ils éclairent la surface du liquide avec les deux lampes situées à une hauteur \(h\) de la surface d'un liquide au repos.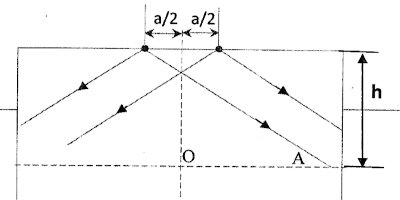
Les lampes sont distantes de \(a\). (figure ci-dessus) Ils constatent qu'un flotteur supposé ponctuel placé au point A est invisible.
Document 1 : Plaque signalétique
Mode par intermittence
Fréquence d’émission des éclairs \(fe = 20Hz\)
Mode continu
Lumière de longueur d’onde \(\lambda = 580nm\)
Informations utiles
La commande est validée lorsque les deux caractéristiques sont conformes.
Le flotteur est invisible lorsqu'il se trouve à un point sombre.
Données: C = 0,4 m/s, OA = 14,925 cm, h = 3m, a = 0,116 cm, d = 20 cm
En exploitant les informations ci-dessus et à l'aide d'une démarche scientifique, I
1. Aide les élèves à vérifier la conformité de la fréquence des éclairs des lampes en mode stroboscopique. 4pt
2. Examine si la commande doit être validée ou non. 4pt