1. Schéma 6 pts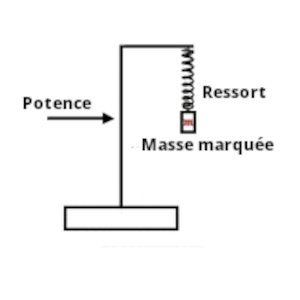
Mode opératoire :
• Accrocher le ressort sur la potence ;
• Accrocher une masse marquée à l’extrémité libre du ressort;
• La masse marquée étant à l’équilibre, la déplacer verticalement (légèrement), puis l’abandonner sans vitesse initiale;
• Mesurer à Paide du chronomètre, le durée de plusieurs, oscillations stables ;
• Diviser la durée obtenue par le nombre d’oscillations pour obtenir la période propre \({T_0}\) correspondant à cette masse marquée ;
• Noter les valeurs de rn et de \({T_0}\) dans un tableau, puis répéter cette opération pour les autres masses marquées.
2. Équation différentielle : \(\ddot x + \frac{k}{m}x = 0\) 2 pts
3. Expression de la période propre \({T_0}\) : \({T_0} = 2\pi \sqrt {\frac{m}{k}} \) 2 pts
4- tableau 0,5x6 = 3 pts
| Masse : m(g) | 120 | 140 | 150 | 160 | 180 | 200 |
| Période : \({T_0}\) | 0,72 0 | 0,775 | 0,790 | 0,818 | 0,866 | 0,924 |
| \(T_0^2({s^2})\) |
0,507 | 0,601 | 0,624 | 0,669 | 0,750 | 0,854 |
5 Tracé de la courbe \(T_0^2 = f(m)\) 4 pts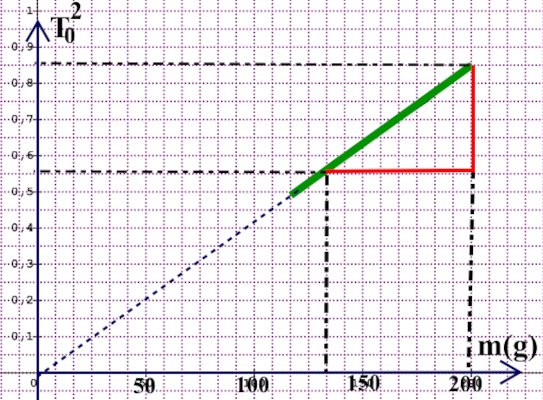 
6. Valeur expérimentale de la constante de raideur \(k\) 3 pts
\(p = \frac{{\Delta T_0^2}}{{\Delta m}} = \frac{{0,51}}{{0,12}}\) \( = 4,25{s^2}k{g^{ - 1}}\)
\(p = \frac{{4{\pi ^2}}}{k} \Rightarrow \) \(k = \frac{{4{\pi ^2}}}{p} = 9,3N.{m^{ - 1}}\)
