Partie A : Évaluation des ressources / 15 points

Exercice I / 3 pts

1. Montrons que la probabilité pour qu'une équation caractéristique de \((E)\) admette deux solutions réelles distinctes ou confondues est de \(\frac{{29}}{{36}}\) 1,5 pt
Une équation caractéristique \({r^2} + 2ar + b = 0\) de \((E)\) admet deux solutions réelles ou confondues si et seulement si \(4{a^2} - 4b \ge 0\), c'est-à-dire que \({a^2} \ge b\)
Tableau de signes de \(4{a^2} - 4b\)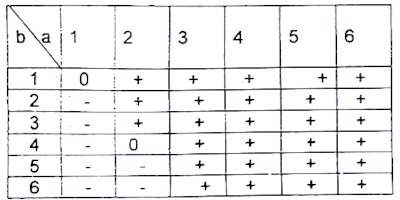
Il y'a 29 couples \((a, b)\) qui vérifient \({a^2} \ge b\), sur un total de 36 Donc cette probabilité est égale \(\frac{{29}}{{36}}\).
2. Déterminons le nombre de fois au minimum dont on doit répéter cette expérience pour être sûr d'avoirr au moins 98% de chances que l'équation caractéristique de \((E)\) ait au moins une fois, deux solutions non réelles.
Désignons par \(n\) ce nombre de fois. Ainsi, on a un schéma de Bernoulli de \(n\) épreuves et dont la probabilité du succès est \(p = 1 - \frac{{29}}{{36}} = \frac{7}{{36}}\)
Avoir au moins une fois deux solutions non réelles c’est, soit 1 fois jusqu’à \(n\) fois et dont la probabilité est \(\sum\nolimits_{k = 1}^n {C_n^k} {\left( {\frac{7}{{36}}} \right)^k}{\left( {\frac{{29}}{{36}}} \right)^{n - k}}\)
Il faut alors que \(\sum\nolimits_{k = 1}^n {C_n^k} {\left( {\frac{7}{{36}}} \right)^k}{\left( {\frac{{29}}{{36}}} \right)^{n - k}} \ge 98\% \). Ce qui est-équivalent à \(1 - C_n^0{\left( {\frac{{29}}{{36}}} \right)^n} \ge \frac{{98}}{{100}}\).
D'où \(n \ge \frac{{\ln 50}}{{\ln 36 - \ln 29}} = 18,09\). Donc le nombre minimum de fois de répéter cette expérience est 19. 1,5 pt

Exercice II / 03 pts

1. Déterminons une base du noyau \(\left( {Ker\varphi } \right)\) de \(\varphi \), puis justifions que \(\varphi \) n'est pas bijectif.
Soit \(\overrightarrow u (x,y,z)\) un vecteur de \({E_3}\).
\(\overrightarrow u \in Ker\varphi \Leftrightarrow \varphi (\overrightarrow u ) = \overrightarrow 0 \) \( \Leftrightarrow \left\{ \begin{array}{l}x + 2y = 0\\2x + y + 3z = 0\\ - x + y - 3z = 0\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}x = - 2y\\z = y\end{array} \right.\).
Donc \(\left( { - 2\overrightarrow i + \overrightarrow j + \overrightarrow k } \right)\) est une base du noyau \(\left( {Ker\varphi } \right)\) de \(\varphi \).
. Puisque \({Ker\varphi \ne \left\{ {\overrightarrow 0 } \right\}}\), alors \(\varphi \) n'est pas bijectif. 1 pt
2.a Montrons que l'image \(\left( {{\mathop{\rm Im}\nolimits} \varphi } \right)\) de \(\varphi \) est un plan vectoriel de \({E_3}\).
On a \(\dim \left( {{\mathop{\rm Im}\nolimits} \varphi } \right) = \dim {E_3}\) \( - \dim \left( {Ker\varphi } \right) = 2\). Ainsi, \({{\mathop{\rm Im}\nolimits} \varphi }\) est un sous espace vectoriel de \({E_3}\) de dimension 2. Donc \({{\mathop{\rm Im}\nolimits} \varphi }\) est un plan vectoriel de \({E_3}\) 0,5 pt
2.b *Vérifions que \(\varphi (\overrightarrow k ) = 2\varphi (\overrightarrow i ) - \varphi (\overrightarrow j )\)
\(2\varphi (\overrightarrow i ) - \varphi (\overrightarrow j ) = \) \(2(\overrightarrow i + 2\overrightarrow j - \overrightarrow k ) - \) \((2\overrightarrow i + \overrightarrow j + \overrightarrow k ) = \) \(3\overrightarrow j - 3\overrightarrow k = \varphi (\overrightarrow k )\) 0,5 pt
2.c. Déduisons-en une base de \({{\mathop{\rm Im}\nolimits} \varphi }\).
\({{\mathop{\rm Im}\nolimits} \varphi }\) est engendrée par \(\varphi (\overrightarrow i )\), \(\varphi (\overrightarrow j )\) et \(\varphi (\overrightarrow k )\). Et donc par \(\varphi (\overrightarrow i )\) et \(\varphi (\overrightarrow j )\) d'après la question 2. b.
Par conséquent, (\(\varphi (\overrightarrow i )\), \(\varphi (\overrightarrow j )\)) constitue une base de \({{\mathop{\rm Im}\nolimits} \varphi }\) qui est un plan vectorielle d après la question 2.a 1 pt

Exercice III / 04 pts

1. Déterminons le sens de variation de \(F\) sur \(\left[ {1; + \infty } \right[\).
\(F\) est dérivable sur \(\left[ {1; + \infty } \right[\) et pour tout \(x \in \left[ {1; + \infty } \right[\), \(F'(x) = f(x)\) et \(f(x)\) est strictement positif sur \(\left[ {1; + \infty } \right[\). Donc \(F\) est strictement croissante sur \(\left[ {1; + \infty } \right[\). 0,25 pt
2.
a. Montrons que pour tout réel \(t \ge 0\), \(t + 2 \ge 2\sqrt 2 \sqrt t \).
Soit \(t - 2\sqrt 2 \sqrt t + 2 = \) \({\left( {\sqrt t - \sqrt 2 } \right)^2}\). D’où \(t - 2\sqrt 2 \sqrt t + 2 \ge 0\). Donc \(t + 2 \ge 2\sqrt 2 \sqrt t \).0,25 pt
b. Déduisons-en que pour tout réel \(x \ge 1\) , \(F(x) \le \frac{1}{{2\sqrt 2 }}\) \(\int_1^x {(t + 2){e^{1 - t}}} dt\) 0,5 pt
2.b soit \(x \ge 1\) et \(t \in \left[ {1;x} \right]\), d’après la question précédente (2.a), on a \(2\sqrt 2 \sqrt t \le t + 2\). D’où \(\int\limits_1^x {2\sqrt 2 \sqrt t {e^{1 - t}}dt} \le \) \(\int\limits_1^x {\left( {t + 2} \right){e^{1 - t}}dt} \) car \({{e^{1 - t}} \succ 0}\), ainsi \(2\sqrt 2 \int\limits_1^x {\sqrt t {e^{1 - t}}dt} \le \int\limits_1^x {(t + 2){e^{1 - t}}dt} \) d’où \(F(x) \le \frac{1}{{2\sqrt 2 }}\int\limits_1^x {(t + 2){e^{1 - t}}dt} \).
3.a. Montrons à l'aide d'une intégration par parties que \(\int\limits_1^x {(t + 2){e^{1 - t}}dt} = \) \(4 - (x + 3){e^{1 - x}}\)
En définissant les fonctions \(u\) et \(v\) par \(u(t) = t + 2\) et \(v'(t) = {e^{1 - t}}\), on a \(\int\limits_1^x {(t + 2){e^{1 - t}}dt} = \) \(4 - (x + 3){e^{1 - x}}\) . 0,5 pt
3.b. Déduisons-en' que pour tout réel \(x \ge 1\), \(0 \le F(x) \le \sqrt 2 \)
Soit un réel \(x \ge 1\). .
D'une part, pour tout \(x \ge 1\), \(f(x) \succ 0\). D'où \(F(x) \ge 0\)
D'autre part, d'après la question 2.b., \(F(x) \le \frac{1}{{2\sqrt 2 }}\int\limits_1^x {(t + 2){e^{1 - t}}dt} \) et d’après la question 3.a.
On a \(F(x) \le \frac{1}{{2\sqrt 2 }}(4 - \) \((x + 3){e^{1 - x}})\) D'où \(F(x) \le \frac{4}{{2\sqrt 2 }}\) car \((x + 3){e^{1 - x}} \succ 0\). Ainsi \(F(x) \le \sqrt 2 \)
Donc pour tout réel \(x \ge 1\), \(F(x) \le \sqrt 2 \) 0,5 pt
4.1. Étudions le sens de variation de la fonction \(f\) sur \(\left[ {0; + \infty } \right[\). 0,5 pt
\(f\) est dérivable sur \(\left[ {0; + \infty } \right[\) et pour tout \(x \succ 0\), \(f'(x) = \frac{{{e^{1 - x}}}}{{2\sqrt x }}\left( {1 - 2x} \right)\). Donc \(f\) est strictement croissante sur \(\left[ {0;\frac{1}{2}} \right]\), et strictement décroissante sur \(\left] {\frac{1}{2}; + \infty } \right[\).
2. Montrons que pour tout entier naturel \(n\), \(f(n + 1) \le {u_n} \le f(n)\)
Soient \(n\) un entier naturel non nul et un réel \(t \in \left[ {n;n + 1} \right]\)
Ainsi \(n \le t \le n + 1\), ce qui .entraine \(f(n + 1) \le f(t) \le f(n)\) car \(f\) est .décroissante sur \(\left] {\frac{1}{2}; + \infty } \right[\) qui contient \(\left[ {n;n + 1} \right]\). D’où \(\int\limits_n^{n + 1} {f(n + 1)} dt \le \) \(\int\limits_n^{n + 1} {f(t)} dt \le \int\limits_n^{n + 1} {f(n)} dt\)
Donc \(f(n + 1) \le \int\limits_n^{n + 1} {f(t)} dt \le f(n)\)
43. (i) Déduisons-en que la suite \(u\) est décroissante.
Soit \(n\) un entier naturel.
\(f(n + 2) \le {u_{n + 1}} \le f(n + 1)\) et \(f(n + 1) \le {u_n} \le f(n)\) d’après la question 4.2.
Ainsi \({u_{n + 1}} \le {u_n}\).
Donc la suite \(\left( {{u_n}} \right)\) est décroissante.
4.3. (ii) Déduisons-en que la suite \(u\) est convergente. 0,5 pt
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^{\frac{1}{2}}}}}{{{e^x}}} = 0\) d'après les croissances comparées. D'où ' \(\mathop {\lim }\limits_{x \to + \infty } f(n) = \mathop {\lim }\limits_{x \to + \infty } f(n + 1)\), ainsi \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = 0\). Donc la suite \(u\) est convergente.
N.B : On remarque aussi que la suite \(u\) est décroissante et minorée par 0. Donc converge.

Exercice IV / 05 points

1. Montrons que l’équation de \(\left( \Gamma \right)\) peut encore s'écrire : \(\frac{{{{\left( {x - 1} \right)}^2}}}{\alpha } - \frac{{{y^2}}}{\beta } = 1\) ou \(\alpha \) et \(\beta \) sont deux réels strictement positifs que nous déterminerons. 1 pt
Soit \(M(x; y)\) un point du plan complexe rapporte au repère \(\left( {O;\overrightarrow u ,\overrightarrow v } \right)\). 1 pt
\(M(x,y) \in \left( \Gamma \right) \Leftrightarrow \) \(3{x^2} - {y^2} - 6x - 1 = 0\)
\(3{x^2} - {y^2} - 6x\) \( - 1 = 0 \Rightarrow 3{(x - 1)^2}\) \( - {y^2} = 4\) \( \Rightarrow \) \(\frac{{{{(x - 1)}^2}}}{{\frac{4}{3}}} - \frac{{{y^2}}}{4} = 1\)
Donc \({\alpha = \frac{4}{3}}\) et \({\beta = 4}\)
2. Déduisons-en que \(\left( \Gamma \right)\) est une hyperbole dont nous déterminerons le centre et les sommets par leurs coordonnées dans le repère \(\left( {O;\overrightarrow u ,\overrightarrow v } \right)\) 1 pt
• \(\left( \Gamma \right)\) est une hyperbole de par la forme de son équation réduite.
• Les coordonnées de son centre sont : \((1;0)\).
• Les coordonnées des sommets sont \(\left( {\frac{{2\sqrt 3 }}{3} + 1,0} \right)\) et \(\left( { - \frac{{2\sqrt 3 }}{3} + 1,0} \right)\)
3. Déterminons la demi distance focale et l’excentricité de \(\left( \Gamma \right)\) 0,5 pt
• La demi-distance focale est \(\sqrt {\frac{4}{3} + 4} = \frac{{4\sqrt 3 }}{3}\)
• L'excentricité est \(\frac{{\frac{{4\sqrt 3 }}{3}}}{{\frac{{2\sqrt 3 }}{3}}} = 2\)
4.1 Donnons la nature et les éléments caractéristiques de S. 1 pt
Nature : S est une similitude plane directe.
Éléments caractéristiques : rapport = 2 ; angle \(\frac{\pi }{6}\) (modulo \({2\pi }\)) ; centre d'affixe : \(\frac{{1 - \sqrt 3 + i}}{{1 - 2{e^{i\frac{\pi }{6}}}}} = 1\)
4. 2.a. Montrons que N est l'image de M par une transformation du plan dont nous donnerons la nature et les éléments caractéristiques. 1 pt
On a \(IN = 2IM\) et \(Mes\left( {\overrightarrow {IM} ;\overrightarrow {IN} } \right) = \frac{\pi }{6}\) deux ëgalités montrent que N est l'image de M par la similitude directe plane de centre I, de rapport 2 et d'angle \(\frac{\pi }{6}\), Il s'agit de la similitude S.
4. 2. b. Déduisons-en la nature de l'ensemble \(\left( {\Gamma '} \right)\) décrit par N lorsque le point M décrit l’ensemble \(\left( {\Gamma } \right)\), puis précisons l’excentricité de \(\left( {\Gamma '} \right)\). 0,5 pt
\(\left( {\Gamma '} \right)\) est une hyperbole.
Son excentricité est égale 2.

Partie B : Évaluation des compétences 05 points

Tâche 1 : Déterminons le temps minimum après lequel on doit administrer ce produit aux maquereaux.
• Déterminons la quantité \({Q_n}\) de maquereaux dans l'étang 1 après \(n\) mois.
Les quantités \({Q_n}\) sont des termes d’une suite géométriques de premier termes \({Q_0} = 250\) et de raison 1,2 : \({Q_n} = 250 \times {\left( {1,2} \right)^n}\)
• Déterminons le minimum de mois après lesquels cette quantité aura au moins doublé.
Cette-quantité aura au moins doublé si et seulement si \({Q_n} \ge 2 \times {Q_0}\)
Dou \(250 \times {\left( {1,2} \right)^n} \ge 2 \times 250\) ainsi \(n \ge \frac{{\ln 2}}{{\ln 1,2}} = 3,8\)
Donc, c’est après au moins 4 mois qu’on doit administrer ce produit aux maquereaux.

Tâche 2 : Déterminons le temps minimum après lequel on doit administrer ce produit aux carpes.
• Déterminons la quantité \(Q(t)\) carpes dans l'étang 2 après \(t\) mois.
La vitesse d’accroissement \(Q'(t)\) des carpes à un instant \(t\) étant le cinquantième de leur quantité \(Q(t)\) au même instant, alors \(Q'(t) = \frac{1}{5}Q(t)\).
D'où \(Q(t) = k{e^{\frac{1}{{50}}t}}\) et puisque \(Q(0) = 450\) Alors \(Q(t) = 450{e^{\frac{1}{{50}}t}}\)
• Déterminons le minimum de mois après lequel cette quantité aura au moins doublé.
Cette quantité aura au moins doublé si et seulement si \(Q(t) \ge 2Q(0)\)
D'où \(450{e^{\frac{1}{{50}}t}} \ge 2 \times 450\), ainsi \(t \ge 50\ln 2\), c'est'-à-dire \(t \ge 34,65\).
Donc, c'.est après au moins» 35 mois qu'on doit administrer ce produit aux carpes.

Tâche 3 : Vérifions si le restaurateur a au moins une chance sur deux de servir les deux clients dans l'ordre des commandes passées.
En suivant la consigne principale de ce restaurant-qui consiste à servir les clients-dans l'ordre de passage de leurs commandes (voir situation), la probabilité de servir des deux clients dans l'ordre des commandes passées est 1.
Le restaurateur a ainsi 100% de chance de servir ces -clients dans l'ordre. Donc au moins une chance sur deux.
N.B. Le texte lié à cette tâche présente des données superflues et quelques insuffisances.