Partie A : Évaluation des ressources 15 points
Exercice I 3,5 pts
1) Résolvons dans C, l’équation z2−(5−3i)z+4−7i=0 1,5 pt
Δ=−2i=(1−i)2
Les solutions de l’équation sont :
z1=5−3i−1+i2=2−i et z2=3−2i
2) Déterminons l’expression complexe de la similitude directe s de centre C qui transforme A en en B 1 pt
Les points A, B et C ont pour affixes respectives zA=2−i, zB=3−2i et zC=1−2i. L’expression complexe de la similitude directe est de la forme z′=az+b avec a et b des nombres complexes.
s(C)=C et s(A)=B soit {a(1−2i)+b=1−2ia(2−i)+b=3−2i ⇒{a=1−ib=2+i
L’expression complexe est z′=(1−i)z+2+i.
3) Précisons les éléments caractéristiques de la similitude s. 0,5 pt
La similitude direct s est de centre C, de rapport k=|1−i|=√2 et d’angle θ=arg(1−i)=−π4 rad
4) Déterminons l’image de la droite (AC) par la similitude s 0,5 pt
L’image de la droite (AC) est donc la droite (BC).
Exercice 2 / 3 points
1) Indiquons toutes les valeurs possibles de X.
Les valeurs cherchées sont : 0, 500, 1000 et 1500
2) Dressons le tableau de la loi de probabilité de X
Cas ou les deux billets sont tirés simultanément
P(X=0)=C216C220=120190
P(X=500)=C13C116C220=48190
P(X=1000)=C11C116+C13C220=19190
P(X=1500)=C11C13C220=3190
Cas ou les deux billes sont tires successivement et sans remise
P(X=500)=A216A220=240380=120190
P(X=500)=A13A116A220×2 =96380=48190
P(X=1000)=A11A116×2+A23A220 =38380=19190
P(X=1500)=A11A13A220×2 =6380=3190
| xi | 0 | 500 | 1000 | 1500 |
| P(X=xi) | 48190, | 48190, | 3190 | 3190 |
3. Calculons la probabilité pour que ce joueur puisse gagner un montant supérieur à 500 francs. 0,5 pt
Il s'agit de calculer P(X≻500)
P(X≻500)=P(X=1000) +P(X=1500)=22190≈0,115
Exercice 3 5 points
a) Résolvons l’équation différentielle (E) : y″+4y′+4y=0. 1 pt
Une équation caractéristique de (E) est : r2+4r+4=0 qui admet la solution double r=2.
Les solutions de l’équation (E) sont des fonctions f(a,b) définies par : f(a,b)(x)=(ax+b)e−2x, a et b étant des constantes réelles.
1 b) Résolvons l’équation différentielle (E) : y″+4y′+4y=−4
Les fonctions g(a,b)(x) solutions de (E′) sont telles que g(a,b)(x)=f(a,b)(x)+γ avec γ∈R on a donc
g′′(a,b)(x)+4g′(a,b)(x) +4g(a,b)(x)=−4 soit 4γ=−4⇒γ=−1.
Donc g(a,b)(x)=(ax+b)e−2x−1
2) g est la fonction définie de R dans R par : g(x)=−1−(x+0,5)e−2x
a) Démontrons que g est la solution de l’équation (E′) vérifiant les égalités g(0)=1,5 et g′(0)=0 0,5 pt
La dérivée de g est g′ définie par g′(x)=2xe−2x et la dérivée de g′ est g” définie par g″(x)=(−4x+2)e−2x
On a g″(x)+g′(x) +g(x)=−4
Donc g est une solution de (E'). En outre g(0)=−1−0,5=−1,5 et 0g′(0)=0
b) Calculons les limites de g en −∞ et +∞; puis déduisons-en une équation d'une asymptote à la courbe de g 0,75 pt
limx→−∞g(x)=+∞ et limx→+∞g(x)=−1 , y=−1 est donc une équation d'une asymptote horizontale à (Cg)
c) Déterminons le signe de g′(x) et dressons le tableau de variations de g. 0,75 pt
g′(x)=2xe−2x et comme pout tout x∈R, e−2x≻0 alors le signe de g′(x) depend du signe de x.
Ainsi pour x∈]−∞;0], g′(x)≤0 et pour x∈[0;+∞[,g′(x)≥0. Le tableau de variation est le suivant : 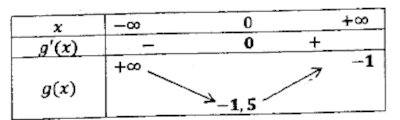 d)` Traçons la courbe de g(x) 1 pt
d)` Traçons la courbe de g(x) 1 pt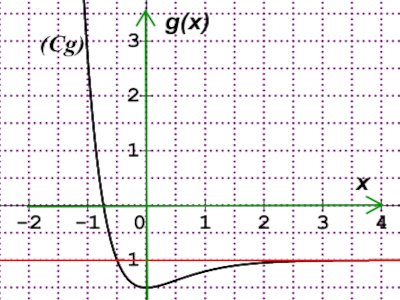 a) Déterminons à l’aide d'une intégration par parties 2∫0(x+0,5)e−2xdx 0,5 pt
a) Déterminons à l’aide d'une intégration par parties 2∫0(x+0,5)e−2xdx 0,5 pt
Posons {u(x)=x+0,5v′(x)=e−2x avec {u′(x)=1v′(x)=−12e−2x
on a 2∫0(x+0,5)e−2xdx=1−3e−12
Exercice 4 3,5 pts
1) Démontrons que la valeur exacte de α est 2 1 pt
Le point moyen G(¯x,¯y) avec ¯x=15(α+8) et ¯y=5,4 appartient à la droite de régression de Y en X d’équation y=3,6x−1,8
On a donc ¯y=3,6¯x−1,8 ⇒¯x=2⇔15(α+8) =2⇒α=2
3) Représentons le nuage des points associés à cette série statistique double.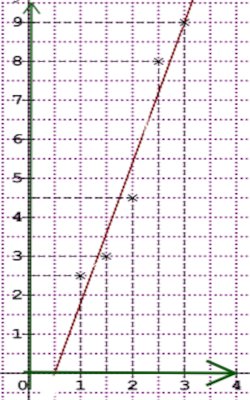 3) Calculons le coefficient de corrélation linéaire σ et donnons une interprétation du résultat obtenu. 1 pt
3) Calculons le coefficient de corrélation linéaire σ et donnons une interprétation du résultat obtenu. 1 pt
σ=cov(x,y)√v(x)×v(y)
Avec cov(x,y)=15∑5i=1xiyi −¯x¯y=635−2×5,4=1,8, V(X)=0,5 et V(Y)=6,94.
On a donc σ=1,8√0,5×6,94≈0,96. On peut dire que la corrélation est bonne car σ=0,96 est une valeur proche de 1.
4) Donnons une estimation du capital de PME au 6ème mois lorsqu'elle avait dépensé 4 millions de francs 0,5 pt
En prenant x=4 dans l’équation de la droite de régression y=3,6x−1,8, on obtient y=12,6
Ceci correspond à un montant de 12.600.000 de francs.
PARTIE B : ÉVALUATION DES COMPÉTENCES 5 pts
Tâche 1 : Déterminons à quelle distance du point O on doit placer le point M pour que l’espace rectangulaire ait une aire maximale.
Posons OM=x avec 0≺x≺100. La longueur du rectangle est L(x)=2x et la largeur est l(x)=√1002−x2. L'aire du rectangle en fonction de x est donnée par : A(x)=2x√1002−x2 =√40000x2−4x4
La dérivée de A est définie par : A′(x)=8x(5000−x2)√40000x2−4x4
A′(x)=0⇒(5000−x2) =0⇒x=50√2 car 0≺x≺100 Le tableau des variations de A est donc 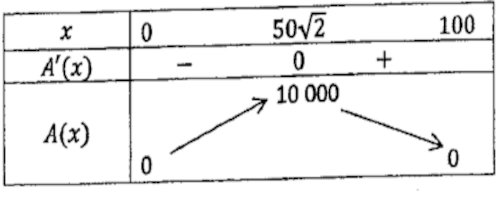 L'aire de l'espace rectangulaire est maximale si OM=50√2=70,7 m.
L'aire de l'espace rectangulaire est maximale si OM=50√2=70,7 m.
Tâche 2 : Vérifions s’il y’a une position du point M pour laquelle la surface rectangulaire est la moitié de la surface initiale du terrain.
On a obtenu A(x)=2x√1002−x2 et l’aire initiale du terrain 12πr2=5000π Si l’aire du terrain rectangulaire est la moitiee de l’aire initiale, on a √40000x2−4x4=2500π, soit x4−1002x2+(2500π)24=0
En posant X=x2, on a X2−1002X+(2500π)24=0
De solutions X1=5000−1250√16−π2 et X2=5000+1250√16−π2
Soient {x1=43,64x2=89,97
On a deux positions possibles du points {OM=43,64OM=89,97.
Tâche 3 : Déterminons à partir de la quatrième année d’épargne si pourra réaliser son projet
Soit un l'avoir de Paul dans cette banque après le 1er Janvier de l année 2016+n.
On a u0=5.000.000 et pour tout entier naturel n, un+1=(1,045)×un. Ainsi la suite (un) est géométrique de raison 1,045 et de premier terme u0=5.000.000. Par suite un=(1,045)n×5.000.000
Pour que Paul soit capable d'investir dans l’élevage, il faut que un≥7.000.000
un=(1,045)n×5.000.000 ≥7.000.000⇒n≥ ln(1,4)ln(1,045)=7,64. La plus petite valeur de n pour la réalisation du projet est 8 pour une épargne égale à u8. Donc le projet est réalisable à partir de la 9ème année.
Présentation 0,5 pt


