Partie A Évaluation des ressources : 15 points

EXERCICE 1 3 points

On considère le tétraèdre régulier ABCD ci-dessous et H le projeté orthogonal de A sur le plan (BCD). I est le milieu de l’aréte [BC].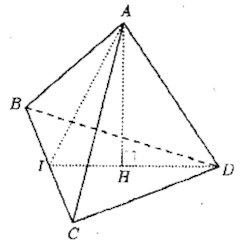
1. a) Démontrer que la droite (BC) est orthogonale au plan (AID). 1 pt
b) Justifier que le peint \(H \in \left[ {ID} \right]\) 0.5 pt
c) En déduire que les droites (BC) et (AH) sont orthogonales 0,5 pt
2. Démontrer que les plans (AID) et (BCD) sont orthogonaux 1pt C

Exercice : 3,5 points

Dans le plan oriente, on considère un rectangle ABCD -tel que \(Mes\left( {\widehat {\overrightarrow {AB} ,\overrightarrow {AD} }} \right) = \frac{\pi }{2}\) et AB = 2AD.
On note I et J les milieux respectifs des segments [AB] et [CD]. On pose \(f = {S_{\left( {IC} \right)}} \odot {t_{\overrightarrow {AB} }} \odot {S_{\left( {IJ} \right)}}\)
1. Caractériser l’isométrie \({t_{\overrightarrow {AB} }} \odot {S_{\left( {IJ} \right)}}\) 0.5 pt
2. En déduire la nature et les éléments caractéristiques de \(f\). 0.75 pt
3. On désigne par K; L et M les points tels que :
\(K = bar\left\{ {(A,2),(C,1)} \right\}\), \(L = bar\left\{ {(A,1),(B,2)} \right\}\), \(M = bar\left\{ {(B,- 4), (C,1)} \right\}\)
a) Montrer que \(B = bar\left\{ {(M,3),(C,1)} \right\}\)0,5 pt
b) i. Montrer que L est le barycentre des points A; M et C affectés des coefficients que l’on précisera. 0,5 pt
ii. En déduire que L est le milieu de [KM] 0.5 pt
4. Déterminer l’ensemble des points N du plan tels que :
\(\left\| {2\overrightarrow {NA} + 3\overrightarrow {NM} + \overrightarrow {NC} } \right\|\) \( = \left\| {\overrightarrow {NA} - \overrightarrow {NB} } \right\|\) 0.75 pt

EXERCICE 3 : 4 points

On considère une fonction numérique \(f\) à variable réelle dont le tableau de variation est ci-dessous.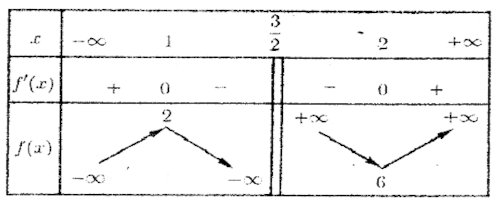
On désigne par (Cf) sa courbe représentative dans le plan muni d’un repère orthonormé \(\left( {O,\overrightarrow i ,\overrightarrow j } \right)\) d’unité 1 cm
1. En vous servant de ce tableau :
a) Déterminer l’ensemble de définition de \(f\) 0,25 pt
b) Déterminer l’ensemble solution de chacune des inéquations suivantes :
i \(f'(x) \le 0\) ; 0,5 pt
ii) \(f(x) \ge 6\). 0,5 pt
2. On donne \(f(x) = \frac{{4{x^2} - 4x - 2}}{{2x - 3}}\)
a) Démontrer que la droite \((D) : y = 2x+ 1\) est une asymptote à (Cf) 0,5 pt
b) Démontrer que le point \(\Omega \left( {\frac{3}{2};4} \right)\) est le centre de symétrie de (Cf) 0,5 pt
3. On désigne par \(g\) la restriction de \(f\) à l’ensemble \(\left[ {1;\frac{3}{2}} \right[ \cup \left] {\frac{3}{2}; + \infty } \right[\)
a) Construire la courbe de la fonction \(g\) 1 pt
b) Déterminer suivant les valeurs du paramétré \(m\), le nombre de solutions dans \(\left[ {1;\frac{3}{2}} \right[ \cup \left] {\frac{3}{2}; + \infty } \right[\) de l’équation \(g(x)= m\) 0,75 pt

EXERCICE : 4 / 4,5 points

Soient \(x \in \mathbb{R}\) et \(\left( {{u_n}} \right)\) la suite numérique définie par \(\left\{ \begin{array}{l}{u_0} = 450\\{u_{n + 1}} = \frac{1}{3}{u_n}{\cos ^2}x + 50{\sin ^2}x\end{array} \right.\) avec \(\forall n \in \mathbb{N}\)
1. a) Démontrer que \(3{\cos ^2}x + {\sin ^2}x = 2\) si et seulement si \({\sin ^2}x = \frac{1}{2}\) 0,5 pt
b) Déterminer dans \(\left] { - \frac{\pi }{2},\frac{\pi }{2}} \right]\) les valeurs de \(x\) pour lesquelles \(3{\cos ^2}x + {\sin ^2}x = 2\), 0,5 pt
2. a) Montrer que \({u_1} = 150{\cos ^2}x + 50{\sin ^2}x\); 0,5 pt
b) Déterminer dans \(\left] { - \frac{\pi }{2},\frac{\pi }{2}} \right]\) les deux valeurs de \(x\) pour lesquelles \({u_1} = 100\). 0,5 pt
3. On prend \(x = \frac{\pi }{4}\) et on définit une nouvelle suite \(\left( {{v_n}} \right)\) par \({v_n} = {u_n} - 30\) , \(\forall n \in \mathbb{N}\)
a) Démontrer que \(\left( {{v_n}} \right)\) est une suite géométrique dont on précisera le premier terme et la raison. 0,75 pt
b) Exprimer \(\left( {{v_n}} \right)\) puis un en fonction de \(n\). 0,5 pt
4. Une machine d’entreprise dispose d'un réservoir ayant 450 titres de carburant. Elle est connectée a un appareil qui chaque jour, ajoute dans le réservoir, systématiquement au démarrage, 25 litres de carburant, et arrête la machine après qu'elle ait consommé les 5/6 du carburant dans le réservoir avant le démarrage.
a. Quelle est la quantité de carburant dans le réservoir à la fin du premier jour de fonctionnement de cette machine. 0,25 pt
b. Déterminer la quantité de carburant dans le réservoir, à la fin du 5ème jour de fonctionnement. 0,5 pt
c. Est-ce possible que cette machine tombe en panne sèche ? Sinon, quelle est la quantité minimale de carburant dans le réservoir a la fin d’un jour de son fonctionnement ? 0,5 pt

PARTIE B. Évaluation des compétences : 5 points

Situation :
Ngoupa est un vernisseur. Il veut savoir à quelle température ramener le vernis, la peinture et le diluant pour obtenir un mélange favorable au bon vernissage du bois d'ébène. Il sait que dans un milieu adiabatique, il obtient un tel mélange à :
• -2°C en combinant 1 titre de vernis, 1 titre de diluant et 1 litre de peinture ;
• 6°c en combinant 4 litres de vernis, 2 litres de diluant et 1 litre de peinture ;
• 0°C en combinant 4 litres de vernis, 3 litres de diluant et 2 litres de peinture.
Pour une commande de vernissage de bois d’ébéne, il a reçu 500 000 FCFA d'un client. Ll estime épargner 320 000 FCFA pour ce travail, et décide alors de faire des placements d'argent dans deux banques différentes.
-Dans la première banque, il place un capital de 240 000 FCFA à un taux d'intérêt annuel de t%. Après un an, le nouveau capital obtenu est ensuite placé à un taux d’intérêt annuel de (t + 4)% et produit un intérêt de 36 960 FCFA.
Dans la deuxième banque, il dépose un capital de 80 000 FCFA qu’il place en deux parts, à des taux différents. La première part, placée au taux d’intérêt annuel le moins élevé, produit après un an, un intérêt de 1 050 FCFA, la seconde part produit un intérêt annuel de 2 250 FCFA après un an. La différence des deux taux est 1%. Il ne se rappelle plus des valeurs de chacune des deux parts placées dans cette banque. .

Tâches: A
1- Pour un litre de chacun des produits : vernis, diluant et peinture, déterminer la température qui convient dans un milieu adiabatique pour obtenir un mélange favorable au vernissage du bois d'ébène. , 1.5 pt
2- Déterminer l’intérêt qu'il aura dans la première banque après un an. 1.5 pt .
3- Déterminer la première part placée dans la deuxième banque. 1.5 pt
Présentation : 0,5 pt