Partie I : Évaluation des ressources / 26 points

Exercice 1 : Vérification des savoirs / 8 points

1.1 Définitions :
Générateur électrique : dispositif capable de transformer toute autre forme d'énergie en énergie électrique. 1 pt
Lentille mince-: lentille dont l'épaisseur est faible devant les rayons de courbure de ses faces. 1 pt
1.2 Énonçons de la loi de Lenz 2 pts
Le sens du courant induit est tel que par ses effets électromagnétiques, il s'oppose toujours à la cause qui lui donne naissance.
1.3 Principe de fonctionnement d'un microscope : 2 pts
Association de deux lentilles convergentes dont l’objectif qui donne d'un objet réel, une image réelle et renversée. Celle-ci devient l’objet pour la deuxième lentille appelée oculaire (loupe). L’image définitive et virtuelle nettement plus grande que l’objet initial.
1.4 Un appareil constitué de lentilles : Microscope, lunette astronomique... 2 pts

Exercice 2 : Application des savoirs / 8 pts

A. Mesures et incertitudes

1. Incertitude élargie 1,5 pt
$U = ku$,
AN : $U = 2 \times 0,15 = 0,30W$
2. Expression du résultat: 1,5 pt
$P = (10,6 \pm 0,3)W$ ou $10,3W \le P \le 10,6W$

B. Induction électromagnétique

1. Flux magnétique 1 pt

$\Phi = NBS$
AN : $\Phi = 1000 \times 0,5 \times 78,5$ $= 3,925Wb$
2.
2.1 Détermination de la variation du flux : 1 pt
$\Delta \Phi = {\Phi _f} - {\Phi _i}$
AN : $\Delta \Phi = 0 - 3,925 = - 3,925Wb$
2.2 Calcul de la f.e.m d'induction : 1,5 pt
$e = - \frac{{\Delta \Phi }}{{\Delta t}}$
AN : $e = - \frac{4}{{0,1}} = - 40V$
2.3 Calcul de l'intensité du courant induit: 1,5pt
$i = \frac{e}{R}$
AN : $i = \frac{{ - 40}}{{50}} = - 0,8A$

Exercice 3 = Utilisation des savoirs /8 points

A. Œil réduit

1. Nature des verres correcteurs : lentilles convergentes 1 pt
2. Vergence de la lentille de contact: 3 pt
$- \frac{1}{{\overline {OA} }} + \frac{1}{{\overline {OA'} }} = C$
$\left\{ \begin{array}{l}OA = - 0,25m\\OA' = - 5m\end{array} \right. \Rightarrow C = 3,8\delta$

B. Caractéristiques d’un générateur

1. Deux éléments du circuit permettant de prendre ces-mesures :voltmètre, ampèremètre, multimètre. 0,5x2= 1 pt
2. Valeur de la f.e.m du générateur: 1 pt
$E = 20,00V$
l 3. Résistance interne du générateur :
• Première méthode : le candidat choisit deux points, calcule la pente et déduit la valeur de $r$.
$r = - \frac{{\Delta U}}{{\Delta I}}$
• Deuxième méthode:
Le candidat calcule la valeur de $r$ correspondant a chaque couple de valeur $(I,U)$, ll obtient le tableau suivant en utilisant la relation $r = \frac{{E - U}}{I}$.
Il calcule la valeur moyenne de $r$. $r = 0,94\Omega$

PARTIE II : ÉVALUATION DES COMPÉTENCES 16 points

1 Il s'agit de déterminer la hauteur maximale atteinte par la locomotive avec la force ${F_m}$ en l’absence des frottements afin de se prononcer sur la déclaration de NGADI.
Pour cela, nous allons :
(i) Faire l’inventaire des forces qui s'exercent sur la locomotive entre A et B, puis entre B et C;
(ii) Appliquer le TEC (ou la conservation de l’énergie mécanique) entre les points A et B, puis. A entre B et C afin de déterminer la hauteur maximale H atteinte;
(iii) Comparer H et h, puis conclure.
Inventaire des forces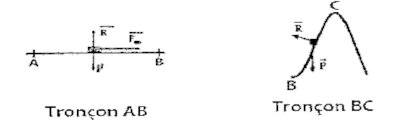
Application du TEC
Entre A et B :
${E_{{C_B}}} - {E_{{C_A}}} = \sum {W({{\overline F }_{ext}})}$
${E_{{C_B}}} - {E_{{C_A}}} = W(\overrightarrow P )$ $+ W(\overrightarrow R ) + W({\overrightarrow F _m})$
$\frac{1}{2}mV_B^2 = {F_m}AB$ (1)
Entre B et C:
${E_{{C_C}}} - {E_{{C_B}}} = \sum {W({{\overline F }_{ext}})}$
${E_{{C_C}}} - {E_{{C_B}}} = W(\overrightarrow P ) + W(\overrightarrow R )$
$\frac{1}{2}mV_B^2 = mgH$ (2)
En combinant (1) et (2), on obtient:
$H = \frac{{{F_m}AB}}{{mg}}$
AN : $H = 116,67m$
Comparaison et conclusion
$H \prec 139m$, donc NGADi n'a pas raison (même en l’absence des frottements, la locomotive ne peut atteindre le sommet)
2. Il s'agit de déterminer l'intensité minimale de la force motrice $F{'_m}$ pour atteindre le point C afin d'examiner la proposition de BAPA.
Pour: cela, nous allons:
Faire l’inventaire des forces qui s'exercent sur la locomotive entre B et C;
(ii) Appliquer le TEC (ou la conservation de
L’énergie mécanique) entre Les points B et C pour déterminer la vitesse ${V_B}$ de la locomotive en B ;
(iii) Faire l'inventaire des forces qui s'exercent sur la locomotive entre A et B ;
(iv) Appliquer le TEC (ou la conservation de l’énergie mécanique) entre les points A et B pour déterminer l’intensité $F{'_{\min }}$;
(v) Comparer $F{'_{\min }}$ à ${F_{\min }}$.
(vi) Conclure.
Inventaire des forces entre B et C
Système : locomotive›
Forces extérieures : le poids de la locomotive et la réaction du support.
Application du TEC entre B et C
${E_{{C_C}}} - {E_{{C_B}}} = \sum {W({{\overline F }_{ext}})}$
${E_{{C_C}}} - {E_{{C_B}}} = W(\overrightarrow P ) + W(\overrightarrow R )$
$- \frac{1}{2}mV_B^2 = - mgH$
Soit ${V_B} = \sqrt {2gh}$. AN : ${V_B} = 52,73m.{s^{ - 1}}$
Inventaire des forces rentre A et B
Système : locomotive
Forces extérieures : le poids de la locomotive, la force motrice et la réaction du support.
Application du TEC entre A et B
${E_{{C_C}}} - {E_{{C_B}}} = \sum {W({{\overline F }_{ext}})}$
${E_{{C_C}}} - {E_{{C_B}}} = W(\overrightarrow P ) + W(\overrightarrow R )$ $+ W({\overrightarrow {F'} _{\min }})$
$\frac{1}{2}mV_B^2 = F{'_{\min }}AB$ $\Rightarrow F{'_{\min }} = \frac{1}{{2AB}}mV_B^2$
AN : $F{'_{\min }} = 834,1N$
Comparaison :
$F{'_{\min }} = 834,1N$
Conclusion: BA.PA a raison