Partie A : Évaluation des ressources (15 pts)

Exercice 1 : 5 ,5 pts

I- Pour chacune des questions suivantes, recopions le numéro de la question suivi de la lettre correspondant à la réponse juste. 3 pts

Il- 1. Déterminons le triplet \(\left( {x,y,z} \right)\)de réels solution du système \(\left\{ \begin{array}{l}2x + y + 2z = 38\\x + y + z = 23\\2x + 2y + z = 37\end{array} \right.\) 1,25 pt
\(\left\{ {\begin{array}{*{20}{l}}{2x + y + 2z = 38({E_1})}\\{x + y + z = 23({E_2})}\\{2x + 2y + z = 37({E_3})}\end{array}} \right. \Rightarrow \) \(\left\{ {\begin{array}{*{20}{l}}{2x + y + 2z = 38}\\{ - y = - 8\left[ {{E_1} - 2{E_2}} \right]}\\{ - y + z = 1\left[ {{E_3} - {E_1}} \right]}\end{array}} \right. \Rightarrow \) \(\left\{ \begin{array}{l}x = 6\\y = 8\\z = 9\end{array} \right.\)
\(S = \left\{ {\left( {6;8;9} \right)} \right\}\)
2- Déterminons le prix de vente de chaque animal.
Choix des inconnues : soient \(𝑥\) prix du coq , \(𝑦\) prix de la pintade, \(𝑧\) prix de la chèvre.
D'après les hypothèses de l’exercice, on le système \(\left\{ {\begin{array}{*{20}{l}}{2x + y + 2z = 3800}\\{x + y + z = 2300}\\{2x + 2y + z = 3700}\end{array}} \right.\), on en déduit ainsi que le prix du coq est de 6000 FCFA celui de la pintade est de 8 000FC FA et pour la chèvre est de 9000 FCFA.

Exercice 2 : 5,5 points

Le plan est rapporte à un repère orthonormé \(\left( {O,I,J} \right)\). Unités sur les axes : 1cm.
On considère la fonction \(f\) définie sur \(\left] {0, + \infty } \right[\) par \(f(x) = x - 1 - 2\ln x\). \((C)\) sa courbe représentative dans le repère \(\left( {O,I,J} \right)\).
1.a) Vérifions que pour tout \(x \in \left] {0, + \infty } \right[\), \(f(x) = x\left( {1 - \frac{1}{x} - 2\frac{{\ln x}}{x}} \right)\) et calculer la limite de \(f\) en \({ + \infty }\) 0,5 pt
\(x\left( {1 - \frac{1}{x} - 2\frac{{\ln x}}{x}} \right) = \) \(x - \frac{x}{x} - 2x\frac{{\ln x}}{x} = x - 1\) \( - 2\ln x = f(x)\).
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \) \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } 2\frac{{\ln x}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{x} = 0\\\mathop {\lim }\limits_{x \to + \infty } x = + \infty \end{array} \right.\) \( \Rightarrow \mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \).
b) Montrons que \(\mathop {\lim }\limits_{x \to {0^{}}} f(x) = + \infty \) puis en donnons une interprétation graphique. 0,5 pt
\(f \) est dérivable sur \(\left] {0, + \infty } \right[\) comme somme de fonctions dérivables sur \(\left] {0, + \infty } \right[\), ainsi pour tout \(x \in \left] {0, + \infty } \right[\),
\(f'(x) = 1 - \frac{2}{x} = \frac{{x - 2}}{x}\)
b) Dressons le tableau des variations de la fonction \(f\).
\(f'(x) = 0 \Ri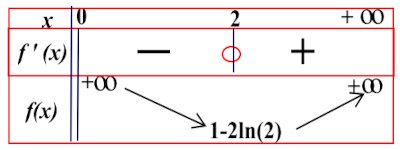ghtarrow x = 2\)
3. Écrirons une équation cartésienne de la tangente \((T) \) à \((C)\) au point d'abscisse 1. 0,75 pt
\(\left( T \right):y = f'(1)(x - 1)\) \( + f(1) = - x + 1\)
4-.a} Recopions et complétons le tableau ci-dessous.
b) Tracer \((C)\) et \((T)\) dans le repère \((O, I, J)\). 1,25pt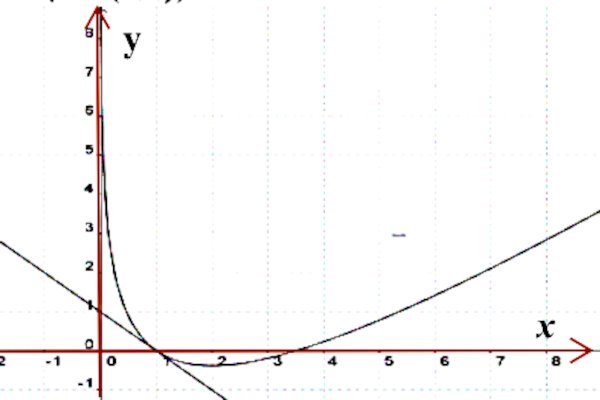

Exercice 3 : 4 points

Dans un pays, une étude est menée durant huit ans sur les moyennes générales en mathématiques aux baccalauréats littéraires. Les résultats sont consignés dans le tableau.
1. Représentons le nuage de points de cette série statistique dans un repère orthogonal. 1 pt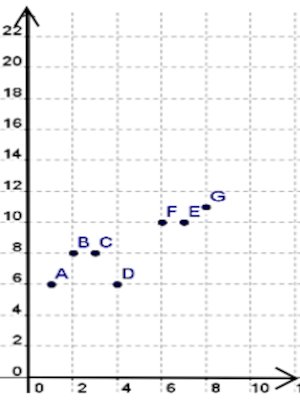
2. Calculons les coordonnées du point moyen G. 1 pt
\(G\left( \begin{array}{l}\overline x = 4,5\\\overline y = 8,5\end{array} \right)\) avec \(\overline x = \frac{1}{8}\sum\nolimits_{i = 1}^8 {{x_i}} \) et \(\overline y = \frac{1}{8}\sum\nolimits_{i = 1}^8 {{y_i}} \)
3. Montrons que la droite de Mayer de cette série statistique a pour équation : \(y = \frac{3}{4}x + 5,125\) 1pt
Considérons les tableaux de deux séries statistiques suivantes :
Tableau de la série 1

Tableau de la série 2

Les points moyen des séries 1 et 2 sont donnés respectivement par \({G_1}\left( \begin{array}{l}2,5\\7\end{array} \right)\) et \({G_2}\left( \begin{array}{l}6,5\\10\end{array} \right)\)
Soit \(M(x,y) \in ({G_1}{G_2})\) alors \(\det \left( {\overrightarrow {{G_1}M} ,\overrightarrow {{G_1}{G_2}} } \right) = 0 \Leftrightarrow \) \(3(x - 2,5) - 4(y - 7) = 0\) \( \Rightarrow y = \frac{3}{4}x + 5,125\).
4. Donnons une estimation de la moyenne en Mathématiques à la 11ème année. 1 pt
\(y = \frac{3}{4} \times 11 + 5,125 = 13,375\)

Partie B : Évaluation des compétences 5 pts

Tâche 1 : vérifions si ces cordes pourront-elles permettre à Ali de puiser de Peau de ce puits.
Soient \(x\) le nombre de cordes de 2m et \(y\) le nombre de Cardenas.
D'après les hypothèses de la compétence, on obtient le système \(1100x + 1200y = \) \(10000 - 500 - 2700\) et \(x = 2y\), soit le système \(\left\{ \begin{array}{l}11x + 12y = 68\\x - 2y = 0\end{array} \right.\) en résolvant ce système, nous trouverons \(\left( {x,y} \right) = \left( {4,2} \right)\). Ainsi il a acheté 2 cardenas et 4 cordes de longueurs de 2m ce qui fera une longueur totale de \(4 \times 2 = 8 \prec 10\)m donc ces cordes ne suffiront pas.

Tâche 2 Vérifions si cet agent pourra aider ALI
Soit \( 𝑥\) ce premier salaire. Après la première hausse, ce salaire en fonction de \(𝑥\) est : \(x + 0,05x = 1,05x\). Après la deuxième hausse, ce salaire en fonction de \(𝒙\) 𝒆𝒔𝒕 ∶ \(1,05x + 0,05 \times 1,05x\) \( = 1,1025x\). Après les deux hausse, son salaire actuel est de 41895, on obtient \(1,1025x = 41895\).
Soit \(x = 38000 \succ 36000\) F CFA. Donc cet agent pourra aider Ali.

Tâche 3 Vérifions si Noé pourra transporter les enfants
Soient \(𝑥\) le nombre d’enfants et \(𝑦\) la part de bonbon reçu par chaque enfant. D’après les hypothèses de la compétence on obtient le \(\left\{ \begin{array}{l}(x - 2) \times (y + 5) = 120\\x \times y = 120\end{array} \right.\) en résolvant ce système, on trouvera \((x,y) = (8,15)\). Donc le nombre d’enfant est 8 ce qui entraîne que Noé ne pourra les transporter.