Problème No 1 (10 pts)
Alima et Sali ont reçu la parcelle ci-dessous représentée comme héritage de leurs parents. Ils veulent se partager équitablement ce let pour le mettre en valeur et ne savent comment s'y prendre.
l. Traçons une droite qui divise ce terrain en deux parties égales. (2 pts)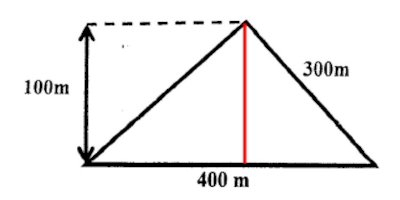
2- Cette droite représente la hauteur de ce triangle. (3 pts)
3. Chacun de ces enfants veut sécuriser son lot avec une rangée de fils barbelés dont le mètre coute 375 F. Calculons la dépense de chacun.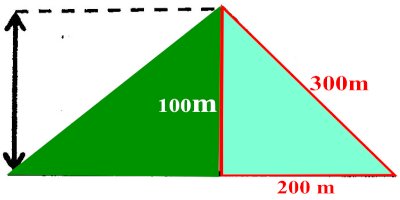
Pour calculer la dépense, il faut connaître le périmètre de chaque lot. Comme chaque enfant obtient une moitié du triangle, ils auront chacun une partie du périmètre total du triangle.
P = 200 +100+300 = 600 m 5 pts
Calcule du cout : C = 600 x 375 = 225 000 F
Problème No 2 (10 pts)
Le Maire de votre localité voudrait distribuer du sucre aux élèves de ton école. Il a une caisse en forme de parallélépipède de 128 cm de long, 48 cm de large et 24 cm de hauteur qui lui permettra de transporter ce sucre. Il sait qu’un paquet de sucre mesure 16 cm de long, 8 cm de large et 6 cm de hauteur, mais il ignore le nombre de paquets de sucre que la caisse peut contenir.
Sers-toi de tes connaissances sur le rangement puis résous le problème.
1- Calculons le nombre de paquets de sucre dans le sens de la longueur. (2 pts)
• Longueur de la caisse : 128 cm
• Longueur d’un paquet de sucre : 16 cm
• Nombre de paquets dans le sens de la longueur :
\(\frac{{128}}{{16}} = 8\)
2- Calculons le nombre de paquets de sucre dans le sens de la largeur. (2 pts)
• Largeur de la caisse : 48 cm
• Largeur d’un paquet de sucre : 8 cm
Nombre de paquets dans le sens de la largeur \(\frac{{48}}{{8}} = 6\)
3- Calculons le nombre de paquets de sucre par couche. (2 pts)
• Nombre de paquets par couche = Nombre de paquets dans le sens de la longueur × Nombre de paquets dans le sens de la largeur
• Nombre de paquets par couche : \(8 \times 6 = 48\)
4- Calculons le nombre de couches obtenues. (2 pts)
Hauteur de la caisse : 24 cm
• Hauteur d’un paquet de sucre : 6 cm
• Nombre de couches \(\frac{{24}}{6} = 4\)
5- .Calculons le nombre total de paquets de sucre. (2 pts)
• Nombre total de paquets = Nombre de paquets par couche × Nombre de couches
• Nombre total de paquets \(48 \times 4 = 192\)
Donc, la caisse peut contenir 192 paquets de sucre.
Problème No 3 (10 pts)
Un camion transporte 180 000 L d'essence. Il livre le \(\frac{1}{5}\) de son essence à MRS, les \(\frac{3}{4}\) à Total et le reste à Tradex. En t'appuyant sur tes connaissances sur les mesures de capacité et de volume, réponds aux questions ci-après :
NB : Le sujet n’étant pas très explicite, nous supposons que toutes les fractions sont appliqué sur la quantité totale et non sur le reste après chaque livraison.
1- Quantité d'essence livrée à MRS : (3 pts )
• Le camion livre \(\frac{1}{5}\) de son essence à MRS.
• Quantité livrée à MRS = \( \frac{1}{5} \times 180,000 \) L = ( 36,000 ) L.
2- Quantité d'essence livrée à Total : (3 pts )
Le camion livre \( \frac{3}{4} \) de son essence à Total.
Quantité livrée à Total = \( \frac{3}{4} \times 180,000 \) L = ( 135,000 ) L.
3- Quantité d'essence restante pour Tradex : (3 pts)
Quantité totale d’essence = 180,000 L.
• Quantité livrée à MRS + Quantité livrée à Total = ( 36,000 ) L + ( 135,000 ) L = ( 171,000 ) L.
• Quantité restante pour Tradex = ( 180,000 ) L - ( 171,000 ) L = ( 9,000 ) L.
4- Convertissons la quantité d'essence livrée à la station Tradex en dm3. (1 pt)
• 1 litre (L) = 1 décimètre cube (dm³).
• Quantité livrée à Tradex = ( 9,000 ) L = ( 9,000 ) dm³.
• Donc, le camion a livré 36,000 L à MRS, 135,000 L à Total, et il reste 9,000 L (ou 9,000 dm³) pour Tradex
Problème No 4 (10 pts)
• Éléments des ensembles en extension :
• A représente les lettres du prénom "rachel".
A={r, a, c, h, e, l}.
• B représente les lettres du prénom "solange".
B = {s, o, l, a, n, g, e}
• Intersection et union :
• : Les lettres communes à "rachel" et "solange" sont {a,e,l}
\(A \cap B = \{ a,e,l\} \)
• Toutes les lettres présentes dans les deux prénoms sont {r,a,c,h,e,l,s,o,n,g}
\(A \cup B = \left\{ {r,a,c,h,e,l,s,o,n,g} \right\}\)
• Cardinalité :
• \(CardA = 6\) (le nombre d'éléments dans A).
• \(CardB = 7\) (le nombre d'éléments dans B).
• \(Card\left( {A \cup B} \right) = 10\) (le nombre d'éléments distincts dans l'union).
• Diagramme de Venn :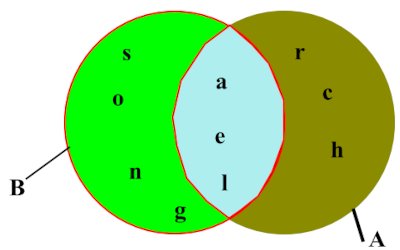 
Problème No 5 (10 pts)
• aux d'intérêt annuel : 6%
• Durée : 4 ans
• Intérêt total après 4 ans : 1 080 000 F
1. Calcul de l'intérêt annuel
L'intérêt total après 4 ans est 1 080 000 F. L'intérêt annuel est donc :
Intérêt annuel = \(\frac{{1080000}}{4} = 270000F\)
2. Calcul de la somme d'argent épargnée (capital initial)
L'intérêt annuel est de 270 000 F, et le taux d'intérêt est de 6%.
Pour trouver le capital initial C, on utilise la formule de l'intérêt simple :
\(C = \frac{{270000 \times 100}}{{6}} = 4500000F\)
3. Calcul du montant total après 1 an et 4 ans
Le montant total après 1 an est la somme épargnée plus l'intérêt de la première année :
Montant apres 1 an =C+Interet annuel =4 500 000+270 000=4 770 000 F.
Le montant total après 4 ans est la somme épargnée plus l'intérêt total après 4 ans :
Montant après 4 ans =C+1 080 000 = 4 500 000+1 080 000=5 580 000 F.
Résumé des réponses :
1. Intérêt annuel : 270 000 F
2. Somme épargnée : 4 500 000 F
3. a) Montant total après 1 an : 4 770 000 F
4. b) Montant total après 4 ans : 5 580 000 F
