La présentation et le soin apporté à la rédaction seront pris en compte dans l’évaluation de la copie.
PARTIE A ÉVALUATION DES RESSOURCES. / 24 points
Exercice 1 : Vérification des savoirs 8 points
1. Définir : Radioactivité ; Fréquence seuil photoélectrique ; Satellite géostationnaire 3 pt
2. Sans démontrer, donner en fonction du champ de pesanteur à la surface de la terre g(0), du rayon moyen de la terre RT et de l’altitude h, l’expression du champ de pesanteur g(h) à l’altitude 0,5 pt
3. Quand dit-on qu’une onde est transversale ? 1 pt
4. Énoncer la loi de la décroissance radioactive 0,5 pt
5. Citer deux applications de la radioactivité. 1 pt
6. Un mobile ponctuel M se déplace sur un axe x’ox d’origine O. la loi horaire de son mouvement est : x(t)=2×10−2cos(40πt−π6)
6.1 Quelle est la nature du mouvement ? Justifier. 1 pt
6.2 Donner la signification de chacun des termes suivants : 2×10−2 40π π6 ; 40πt−π6
Exercice 2 : Application directe des savoirs et des savoir-faire (8 points)
1. Le condensateur 2points
Aux borne d’un condensateur plan de capacité C=100nF on mesure une tension UC=30mV
1.1 Calculer l’énergie emmagasinée par le condensateur 0 ,5 pt
1.2 Déterminer la charge du condensateur 0 ,5 pt
1.3 A l’aide de l’analyse dimensionnelle donner l’unité de la capacité 1 pt
2. Radioactivité : 3 points
Le polonium 21084Po est radioactif α et de période T = 138 jours.
2.1 Écrire l’équation de sa désintégration en précisant les règles utilisées. 1 pt
2.2 A la date t=0, on dispose d’un échantillon pur de polonium 210 de masse m0=10mg.
2.2.1 Déterminer le nombre N0d’atomes de Polonium présents dans cet échantillon. 0,5 pt
2.2.2 Calculer son activité A0 à l’instant initial (t=0). 0,5 pt
On donne : Nombre d’Avogadro : NA=6,02×1023mol−1.
2.3 Quelle masse m de Polonium subsiste-t-il dans l’échantillon à la date t=30 jours ? 0,5 pt
3. Le pendule simple 3 points
Un pendule simple est constitué d’un fil inextensible de masse négligeable et de longueur ℓ = 25 cm et d’une boule quasi-ponctuelle (B) de masse m=50g. Initialement vertical, on écarte le pendule de 8o et on l’abandonne sans vitesse initiale. Les frottements sont négligeables. On repère la position du pendule par son abscisse angulaire θ par rapport à la verticale.
3.1 En appliquant le théorème du centre d’inertie à (B), établir l’équation différentielle régissant le mouvement du pendule.
En déduire la nature de ce mouvement. 1,25 pt
3.2 On prend pour origine des dates la date où le pendule est abandonné à lui-même. Déterminer l’amplitude, la phase initiale et en déduire la loi horaire du mouvement du pendule.
NB : On utilisera la fonction cosinus. 0,75 pt
3.3 A quel instant t1le pendule passe-t-il pour la première fois par sa position d’équilibre ? Calculer sa vitesse linéaire V1 de la boule à cet instant. 1 pt
EXERCICE 3 : Utilisation des savoirs et des savoir-faire (8 points)
1. La lumière 2 points
Une source monochromatique F éclaire deux fentes fines F1 et F2, parallèles, distantes l’une de l’autre de a=3mm. La source est sur la perpendiculaire au plan F1F2 et est équidistante de F1 et F2. On observe des interférences sur un écran E placé à D=3m du plan de F1F2. La distance entre la 6e frange brillante située avant la frange centrale, et la 6e frange brillante située après la frange centrale est L=7,2mm.
1.1 Quelle est la longueur d’onde de la radiation émise par F ? 1 pt
1.2 On utilise maintenant une source lumineuse émettant simultanément deux radiations de longueur λ1=0,55μm et λ2=0,44μm
À quelle distance de la frange centrale se produit la 1ère coïncidence entre les deux systèmes de franges ? 1 pt
2. Mouvement d’un cascadeur 4 points
Un cascadeur, à bord de sa moto Honda CR500, après une phase d’accélération, aborde le tremplin avec une vitesse de 160 km/h et s’envole pour un saut d’une portée CD.
Dans cet exercice, on étudie trois phases du motard (de A à C) :
- La phase d’accélération du motard (de A à B) ;
- La montée du tremplin (de B à C) ;
- Le saut (au-delà de C).
Le système {motard+moto} est assimilé à son centre d’inertie G. On pose h=OC=ED ; g=9,81m/s² ; masse du système : m=180kg ; L=BC=7,86m. Le motard s’élance sur la piste avec une vitesse nulle. Sont représentées ci-dessous les évolutions au cours du temps de la valeur v de la vitesse du motard (figure2) et la distance d qu’il parcours depuis le début du mouvement (figure 3).
Le motard s’élance sur la piste avec une vitesse nulle. Sont représentées ci-dessous les évolutions au cours du temps de la valeur v de la vitesse du motard (figure2) et la distance d qu’il parcours depuis le début du mouvement (figure 3).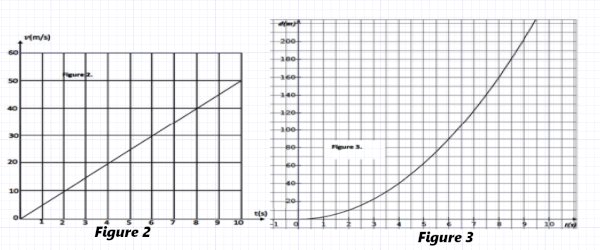 2.1 Montrer que la courbe de la figure 2 permet d’affirmer que la valeur de l’accélération est constante.
2.1 Montrer que la courbe de la figure 2 permet d’affirmer que la valeur de l’accélération est constante.
Déterminer sa valeur. 0.5 pt
2.2 En utilisant la figure 2 et la figure 3, déterminer la distance parcourue par le motard lorsque celui-ci a atteint une vitesse de 160 km/h. 0.5 pt
2.3 Le Motard aborde le tremplin au point B avec une vitesse de 160 km/h et maintient cette vitesse jusqu’au point C. Le tremplin est incliné d’un angle α=27o par rapport à l’horizontale.
Préciser la nature du mouvement du motard sur le parcours BC. 0.5 pt
2.4 En déduire l’équation horaire x=f(t). 0.5 pt
On prendra l’origine des espaces et des dates en B.
2.5 Calculer le temps mis pour parcourir la distance BC. 0.5 pt
2.6 Le motard quitte le tremplin en C avec une vitesse VC=160km/h pour atterrir au point D. L’origine des dates est choisie à l’instant où le système quitte le point C.
2.6.1 Établir les équations horaires du mouvement du motard dans le repère (O,i,j,k). 0.75 pt
2.6.2 Montrer que l’équation de la trajectoire est y=−3,31×10−3x2 +0,51x 0.75 pt
2.6.3 Déterminer la distance CD 0.5 pt
3. Les circuits RLC 2 points
Un générateur entretient entre ses bornes une tension alternative de fréquence 50 Hz et de valeur efficace 24 V. On monte en série entre ses bornes une bobine de résistance R = 80 Ω et un ampèremètre.
L’ampèremètre indique I1=100mA.
3.1 Quelle est la valeur de l’impédance de la bobine (On négligera la résistance interne de l’ampèremètre) 0,5pt
3.2 Quelle est la valeur de l’inductance de la bobine ? 0,5pt
3.3 On monte maintenant entre ses bornes, toujours en série, un condensateur et le même ampèremètre.
L’ampèremètre indique alors une intensité I2=80mA.
3.1 Quelle est la valeur de la capacité de ce condensateur ? 0,5pt
3.2 Quelle est la différence de phase entre la tension et le courant ? 0,5pt
PARTIE B : Évaluation des compétences 16 points
Au cours d’une séance de travaux pratique en classe de Tle D, l’enseignant demande a un groupe d’élève d’identifié le métal donc ils auront besoin pour une épreuve pratique de chimie. Pour cela il met à leur disposition le matériel suivant :
• Une cellule photoélectrique du métal inconnu ;
• Un voltmètre ;
• Un micro-ampèremètre ;
• Un générateur de tension variable E ;
• Une source de laser monochromatique de fréquence variable.
• Un tableau de métaux et de leur fréquence seuil photoélectrique (vs ) ;
| Métal | Métal Argent | Cuivre | Zinc | Potassium | Césium |
| Fréquence de seuil photoélectrique ( ?? ). vs×1014 (Hz) | 11,11 | 10,32 | 8,20 | 5,38 | 14,51 |
A l’aide du matériel disponible, ce groupe d’élève a obtenu les résultats suivants :
| v×1014 (Hz) | 5,50 | 6,10 | 6,25 | 6,45 | 7,20 | 7,60 | 7,75 | 8,65 |
| U0(V) | 0,05 | 0,20 | 0,24 | 0,29 | 0,48 | 0,58 | 0,62 | 0,85 |
1. Expliquer clairement le mode opératoire 6 points
Consigne : On fera le schéma du dispositif expérimental ayant permis l’obtention des résultats consignés dans le tableau ci-dessus.
2. A l’aider d’un raisonnement scientifique, identifier le métal à utiliser durant l’expérience de chimie. 10 points

