Cette épreuve étalée sur deux pages, est constituée de deux parties indépendantes.

Partie A : Évaluation des ressources (15 points)

Exercice 1 : (3,5 points)

Le plan complexe est muni d'un repère orthonormé \(\left( {O;\overrightarrow {{e_1}} ,\overrightarrow {{e_2}} } \right)\).
On considère les points A, B et C d'affixe respectives \({Z_A} = 2 - i\) ; \({Z_B} = 3 - 2i\); et \({Z_C} = 1 - 2i\).
1) Résoudre dans \(\mathbb{C}\), l’équation \({z^2} - \left( {5 - 3i} \right)z\) \( + 4 - 7i = 0\). (1,5 pt)
2) Déterminer l’expression complexe de la similitude directe \(s\) de centre C et qui transforme A en B. (1 pt)
3) Préciser les éléments caractéristiques de \(s\). (0,5 pt)
4) Quelle est l’image de la droite (AC) parla similitude \(s\) ? (0,5pt)

Exercice 2 : (3 points)

Une loterie comporte vingt billets. Parmi eux, il y a un (seul) billet gagnant 1000 francs et trois billets gagnant 500 francs. Les autres billets ne rapportent aucun franc. Les billets gagnants et non gagnants sont indiscernables par le joueur.
Une personne achète deux billets. On considère la variable aléatoire X donnant la somme totale (en francs) que ces deux billets lui rapportent.
1) Indiquer toutes les valeurs possibles de X. (1 pt)
2) Dresser le tableau de la loi de probabilité de X. (1 ,5pt)
3) Quelle est la probabilité pour que ce joueur puisse gagner plus de 500 francs ? (0,5 pt)

Exercice 3 : (5 points) `

On considère sur l'ensemble des nombres réels \(\mathbb{R}\), les équations différentielles
(E) : \(\left( E \right):y'' + 4y' + 4y = 0\) et \(\left( {E'} \right):y'' + 4y' + 4y = - 4\)
Le plan est muni d’un repère orthogonal avec 1 cm pour unité sur l’axe des abscisses (Ox) et 2 cm pour unité sur l'axe des ordonnées (Oy).
1 1) a) Résoudre l’équation \((E)\). (1 pt)
b) Résoudre l’équation \((E')\). (0,5pt)
2) Soit la fonction \(g\) de \(\mathbb{R}\) vers \(\mathbb{R}\) définie par l’égalité \(g(x) = - 1 - \left( {x + 0,5} \right){e^{ - 2x}}\).
a) Démontrer que \(g\) est la solution de l’équation \((E’)\) vérifiant les égalités \(g(0) = - 1,5\)et \(g'(0) = 0\). (0,5pt)
b) Calculer les limites de \(g\) en \( - \infty \) et en \( + \infty \). En déduire une équation d'une asymptote à la courbe \((Cg)\) de \(g\). (0,75 pt)
c) Déterminer le signe de \(g"(x)\) et dresser le tableau de variations de \(g\). (0,75 pt).
d) Tracer la courbe \((Cg)\) dans le plan. (1 pt)
e) Déterminer à l'aide d'une intégration par parties, \(\int_0^2 {\left( {x + 0,5} \right)} {e^{ - 2x}}dx\) . (0,5pt)

Exercice 4 : (3,5 points)

Les dépenses mensuelles \(X\) et les capitaux associés \(Y\) d'une PME de cinq mois consécutifs sont donnés dans le tableau statistique suivant :

\(\alpha \) est un montant masqué par le statisticien qui mentionne néanmoins qu’une équation de la droite de régression de \(Y\) en \(X\) que la valeur exacte de \(\alpha \) a permis d’obtenir est donnée par l’égalité \(y = 3,6x - 1,8\).
1) Démontrer que la valeur exacte de \(\alpha \) est 2. (1 pt)
2) Représenter le nuage de points associé à cette série statistique double. (1 pt)
3) Calculer le coefficient de corrélation linéaire \(r\) et donner une interprétation du résultat obtenu. (1 pt)
4) Donner une estimation du capital de cette PME au 6e mois lorsqu'elle avait dépensé 4 millions de francs. (0,5 pt)

PARTIE B Évaluation des compétences (5 points)

Situation :
Le 1er janvier 2016, Paul a épargné une somme de 5 millions de francs dans une banque où le taux d intérêt annuel composé est de 4,5 %. Il compte vider plus tard ce compte pour investir dans relevage à hauteur de 7 millions de francs.
Paul a dans son village un terrain dont la surface a la forme d’un demi-disque de centre O et de rayon 100 m. Voir figure ci-dessous.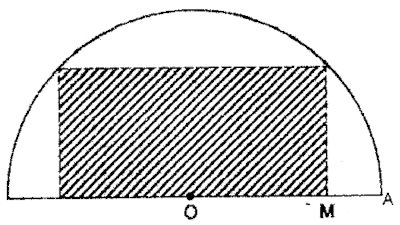
Les points O et A représentent respectivement un oranger et un avocatier situés sur la bordure du terrain.
À partir d'un point M du rayon [OA], il veut protéger une surface rectangulaire (hachurée sur la figure) dont deux de ses sommets sont sur l’arc de cercle.
Cet espace rectangulaire sera exploite pour relevage et financé grâce à l’argent épargné. Paul voudrait que cet espace ait une aire maximale alors que son épouse, qui a besoin du reste du terrain pour l’agriculture, souhaite que l’espace rectangulaire destiné à relevage garde la forme voulue par Paul et soit plutôt la moitié de l’espace total.
En 2020, Paul se demandait déjà si le moment n’était pas venu pour commencer son projet de 7 millions provenant de l’argent épargné.

Tâches:
1) Ã quelle distance du point O doit-on placer le point M pour que l’espace rectangulaire ait une aire maximale ? (1,5 pt)
2) Y a-t-il de positions du point M permettant à la surface rectangulaire d'être la moitié de la surface initiale du terrain ? (1,5 pt)
3) À partir de la quantième année d'épargne, Paul pourra-t-il réaliser son projet ? (1,5 pt)
Présentation : 0,5 pt