PARTIE A. Évaluation des Ressources : 15 points

EXERCICE 1 : 3 points

1. a) Démontrons que la droite $(BC)$ est orthogonale au plan $(AID)$.
$(ID)$ est la hauteur relative à la base $[BC]$ du triangle équilatéral BCD, d'où (BC) et (ID) sont perpendiculaires. En outre, $(IA)$ est la hauteur relative à la base $[BC]$ du triangle équilatéral ABC, d'où $(BC)$ et $(IA)$ sont perpendiculaires. Les droites $(IA)$ et $(ID)$ sont deux droites sécantes du plan $(AID$). Donc la droite $(BC)$ est orthogonale au plan $(AID)$. 1 pt
b) Justifions que le point $H \in \left[ {ID} \right]$. 0,5 pt
$(AH)$ est la hauteur du tétraèdre régulier ABCD, ainsi H est le centre de gravité du triangle équilatéral BCD, d'où H est l’intersection des médianes de BCD parmi lesquelles [ID].
1. c) Déduisons-en que les droites (BC) et (AH) sont orthogonales. 0,5 pt
A D'après les questions précédentes, H est point est du plan (AID), ainsi (AH) est une droite du plan (AID). Puisque (BC) est orthogonale à (AID), alors les droites (BC) et (AH) sont orthogonales.
2. Démontrons que les plans (AID) et (BCD) sont orthogonaux; 1 pt
La droite (BC) est une droite du plan (BCD) et (BC) est orthogonale .au plan (AID), donc les plans (AID) et (BCD) sont orthogonaux.

EXERCICE 2 3,5 points

1. Caractérisons l’isométrie ${t_{\overrightarrow {AB} }} \circ {S_{(IJ)}}$ 0,5 pt
On a : ${t_{\overrightarrow {AB} }} = {S_{(BC)}} \circ {S_{(IJ)}}$ d’où ${t_{\overrightarrow {AB} }} \circ {S_{(IJ)}} =$ ${S_{(BC)}} \circ {S_{(IJ)}} \circ {S_{(IJ)}}$ donc ${t_{\overrightarrow {AB} }} \circ {S_{(IJ)}} = {S_{(BC)}}$ qui est la symétrie orthogonale d'axe (BC).
2. Déduisons-en la nature et les éléments caractéristiques de $f$.0,75 pt
$f = {S_{(IC)}} \circ {t_{\overrightarrow {AB} }} \circ {S_{(IJ)}}$ $= {S_{(IC)}} \circ {S_{(BC)}} = R\left( {C; - \frac{\pi }{2}} \right)$ qui est la rotation de centre C et d'angle ${ - \frac{\pi }{2}}$. 0,75 pt
3. a) Montrons que $B = bar\left\{ {\left( {M,3} \right);\left( {C,1} \right)} \right\}$.
On a : $M = bar\left\{ {\left( {B, - 4} \right);\left( {C,1} \right)} \right\}$ d'où $- 4\overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow O$, qui est équivalent à $4\overrightarrow {BM} - \overrightarrow {BM} + \overrightarrow {BC} = \overrightarrow O$ soit $\overrightarrow {3BM} + \overrightarrow {BC} = \overrightarrow O$ donc $B = bar\left\{ {\left( {M,3} \right);\left( {C,1} \right)} \right\}$ 0,5 pt
3. b) i. Montrons que L est le barycentre des points A; M et C affectés des coefficients que nous préciserons. 0,5 pt
on a : $L = bar\left\{ {\left( {A,1} \right);\left( {B,2} \right)} \right\}$ $= bar\left\{ {\left( {A,2} \right);\left( {B,4} \right)} \right\}$et B = ba.r{(M, 3),(c,1)}, et $B = bar\left\{ {\left( {M,3} \right);\left( {C,1} \right)} \right\}$ d’où $L = Bar\left\{ {\left( {A,1} \right);\left( {M,3} \right);\left( {C,1} \right)} \right\}$
Donc L est le barycentre des points A; M et C affectés des coefficients respectifs 2 ; 3 et 1. 0,5 pt
3.. b) ii. Déduisons-en que L est le milieu de [KM]. 0,5 pt
D'après la question précédente, $L = bar\left\{ {\left( {A,1} \right);\left( {M,3} \right);\left( {C,1} \right)} \right\}$, et par le barycentre partiel $K = bar\left\{ {\left( {A,2} \right);\left( {C,1} \right)} \right\}$, il vient que $L = Bar\left\{ {\left( {A,1} \right);\left( {M,3} \right);\left( {C,1} \right)} \right\}$ $= bar\left\{ {\left( {K,3} \right);\left( {M,3} \right)} \right\}$
Ainsi L est l’isobarycentre des points K et M, donc L est le milieu B de [KM]. 0,5 pt
4. Déterminons l’ensemble des points N du plan tels que : $\left\| {2\overrightarrow {NA} + 3\overrightarrow {NM} + \overrightarrow {NC} } \right\|$ $= \left\| {\overrightarrow {NA} - \overrightarrow {NB} } \right\|$
D'après la question 3 b) i. on a $2\overrightarrow {NA} + 3\overrightarrow {NM} + \overrightarrow {NC}$ $= 6\overrightarrow {NL}$
D'où $\left\| {2\overrightarrow {NA} + 3\overrightarrow {NM} + \overrightarrow {NC} } \right\|$ $= \left\| {\overrightarrow {NA} - \overrightarrow {NB} } \right\| \Leftrightarrow$ $\left\| {6\overrightarrow {NL} } \right\| = \left\| {\overrightarrow {AB} } \right\| \Leftrightarrow$ $LN = \frac{{AB}}{6}$. Donc l’ensemble de ces points N du plan, est le cercle de centre L et de rayon $\frac{{AB}}{6}$. 0,75 pt

EXERCICE 3 4 points

1. En nous servant du tableau de variation de $f$:
a) Déterminons l’ensemble de définition $Df$ de $f$ : $Df = \left] { - \infty ;\frac{3}{2}} \right[ \cup \left] {\frac{3}{2}; + \infty } \right[$ 0,25 pt
. b) Déterminons l’ensemble solution de chacune des inéquations suivantes :
i) $f'(x) \le 0$, $S = \left[ {1;\frac{3}{2}} \right[ \cup \left] {\frac{3}{2};2} \right]$ 0,5 pt
ii) $f(x) \ge 6$, $S = \left] {\frac{3}{2}; + \infty } \right[$ 0,5 pt
a) Démontrons que la droite $\left( D \right):y = 2x + 1$ est une asymptote à $(Cf)$.
En effet :
$\mathop {\lim }\limits_{x \to - \infty } \left[ {f(x) - y} \right] =$ $\mathop {\lim }\limits_{x \to - \infty } \frac{1}{{2x - 3}} = 0$ et  $\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - y} \right] =$ $\mathop {\lim }\limits_{x \to + \infty } \frac{1}{{2x - 3}} = 0$ 0,5 pt
b) Démontrons que le point . $\Omega \left( {\frac{3}{2};4} \right)$ est le centre de symétrie de $(Cf)$.
$x \in Df$, $3 - x \in Df$ et $f(3 - x) + f(x) =$ $\frac{{16x - 24}}{{2x - 3}} = 8 = 2 \times 4$. Donc le point$\Omega \left( {\frac{3}{2};4} \right)$ est le centre de symétrie de (Cf). 0,5 pt
a) Construisons la courbe de la fonction $g$. 1 pt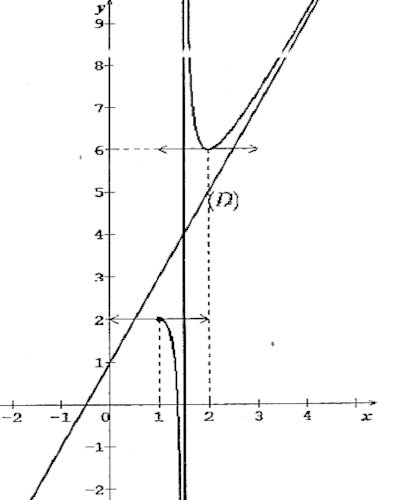
3. b) Déterminons suivant les valeurs du paramètre $m$, le nombre de solutions dans $\left[ {1;\frac{3}{2}} \right[ \cup \left] {\frac{3}{2}; + \infty } \right[$, de l’équation $g(x) = m$. 0,75 pt
• Pour $m \in \left] { - \infty ;2} \right] \cup \left\{ 6 \right\}$, l'équation a une seule solution.
• Pour $m \in \left] {2;6} \right[$, l’équation n'a pas de solution.
• Pour $m \in \left] {6, + \infty } \right[$, l’équation a deux solutions.

EXERCICE 4  4,5 points

a) Démontrons que $3{\cos ^2}x + {\sin ^2}x = 2$ si et seulement si ${\sin ^2}x = \frac{1}{2}$
Soit $x \in \mathbb{R}$
$3{\cos ^2}x + {\sin ^2}x = 2$ $\Leftrightarrow 3(1 - {\sin ^2}x) + {\sin ^2}x = 2$ $\Leftrightarrow - 2{\sin ^2}x = - 1$ alors ${\sin ^2}x = \frac{1}{2}$ 0,5 pt
b) Déterminons dans $\left] { - \frac{\pi }{2},\frac{\pi }{2}} \right]$ les valeurs de $x$ pour lesquelles $3{\cos ^2}x + {\sin ^2}x = 2$.
D’après la question précédente, $3{\cos ^2}x + {\sin ^2}x = 2$ équivaut a ${\sin ^2}x = \frac{1}{2}$, soit a $\sin x = \frac{{\sqrt 2 }}{2}$ ou $\sin x = - \frac{{\sqrt 2 }}{2}$ et donc $x = \frac{\pi }{4}$ ou $x = - \frac{\pi }{4}$. 0,5 pt
2. a) Montrons que ${u_1} = 150{\cos ^2}x + 50{\sin ^2}x$
${u_1} = \frac{1}{3} \times 450{\cos ^2}x + 50{\sin ^2}x$ Donc ${u_1} = 150{\cos ^2}x + 50{\sin ^2}x$ 0,5 pt
b) Déterminons dans $\left] { - \frac{\pi }{2},\frac{\pi }{2}} \right]$; les deux valeurs de $x$ pour lesquelles ${u_1} = 100$
$150{\cos ^2}x + 50{\sin ^2}x$ $= 100 \Leftrightarrow 3{\cos ^2}x +$ ${\sin ^2}x = 2$ D'après la question 1. b), les valeurs de $x$ sont : $x = \frac{\pi }{4}$ et $x = - \frac{\pi }{4}$
a) Démontrons que $\left( {{v_n}} \right)$ est une suite géométrique dont nous préciserons le premier terme et la raison.
Soit $n$ un entier naturel.
${v_{n + 1}} = {u_{n + 1}} - 30 =$ $\frac{1}{6}{u_n} + 25 - 30 = \frac{1}{6}{u_n} - 5 =$ $\frac{1}{6}({u_n} - 30) = \frac{1}{6}{v_n}$. Donc $\left( {{v_n}} \right)$ est une suite géométrique dont le premier terme est ${v_0} = 420$ et la raison $q = \frac{1}{6}$.
3. b) Exprimons ${{v_n}}$, puis ${{u_n}}$ en fonction de $n$.
${v_n} = {v_0} \times {q^n}$ et ${u_n} = {v_n} + 30$. 0,5 pt
4 a. Déterminons la quantité de carburant dans le réservoir à la fin du premier jour de fonctionnement de cette machine.
Cette quantité est égale à : $450 + 25 - \frac{5}{6} \times 450 = 100$, soit 100 litres. 0,25 pt
4. b. Déterminons la quantité de carburant dans le réservoir, à la fin du 5eme jour de fonctionnement. 0,5 pt
Si ${q_n}$ et ${q_{n + 1}}$ désignent respectivement les quantités de carburant dans le réservoir au nieme et le jour suivant, alors ${q_{n + 1}} = {q_n} + 25 -$ $\frac{5}{6} \times {q_n} = \frac{1}{6}{q_n} + 25$. D'après la question 3.b), la quantité de carburant dans le réservoir au 5ème jour de fonctionnement est : $420{\left( {\frac{1}{6}} \right)^n} + 30$. Soit environ 30,054 litres. .0,5 pt
4. c. Étudions 1 la possibilité que cette machine tombe en il panne sèche. Sinon déterminons la quantité minimale de carburant dans le réservoir à la fin d'un jour de son fonctionnement.
Il y'a panne sèche au nième jour si et seulement si $420{\left( {\frac{1}{6}} \right)^n} + 30 = 0$. La quantité $420{\left( {\frac{1}{6}} \right)^n} + 30$ est strictement positive, donc cette machine ne peut pas tomber en panne sèche.
Pour un jour de rang $n$ assez grand, la quantité minimale est 30 litres car $420{\left( {\frac{1}{6}} \right)^n} + 30$ tend vers 0. 0,5 pt

PARTIE B. Évaluation Des compétences / 5 points

Tâche 1 : Pour un litre de chacun des produits : vernis, diluant et peinture, déterminons la température qui convient dans un milieu adiabatique pour obtenir un mélange favorable au vernissage du bois d'ébène.
Pour cette tâche, la situation permet d’obtenir un mélange favorable dans un milieu adiabatique $\theta = - {2^o}C$ en combinant un litre de chacun des produits vernis, diluant et peinture.
NB : La tâche étant mal formulée, attribuer 1 ,5 pt à chaque candidat.

Tâche 2 : Déterminons l’intérêt qu'il aura dans la première banque après un an.
l - Déterminons le taux d'intérêt t%.
Le capital après un an de placement est :
$240000 + 240000 \times \frac{t}{{100}}$ $= 240000 + 2400t$
L'intérêt sur le capital après un an est : $(240000 + 2400t) \times$ $\frac{{t + 4}}{{100}} = 36960$, d’où l’équation : ${t^2} + 104t - 1140 = 0$
Les solutions de cette équation sont: -114 et 10. Donc le taux d'intérêt après un an est 10%.
Déterminons l'intérêt qu'il aura dans la première banque agrès un an.
Cet intérêt est égal à $240000 \times \frac{{10}}{{100}} = 24000$, soit 24 000 FCFA.

Tâche 3 : Déterminons la première part placée dans la deuxième banque.
Déterminons le taux d'intérêt correspondant à la première part,
Désignons par t% ce taux. B
La première part est : $1050 + \frac{t}{{100}} = \frac{{150000}}{t}$ et la deuxième part est : $2250 + \frac{{t + 1}}{{100}} = \frac{{225000}}{{t + 1}}$ Ainsi $\frac{{105000}}{t} + \frac{{225000}}{{t + 1}} = 80000$. D'ou l’équation $16{t^2} - 50t - 21 = 0$ et ses solutions sont $- \frac{3}{8}$ et $\frac{7}{2}$ Donc le taux d'intérêt correspondant à la première part est 3,5%. .
Déterminons la première part placé dans la deuxième banque.
Cette première part est égale à $\frac{{105000}}{{3,5}} = 30000$. soit 30 000 FcFA.

Ou bien : soit $x$ la première part de taux d’intérêt t%. La 2e part est alors
$80000 - x$ de taux d'intérêt (t + 1)%. On a alors $\left\{ \begin{array}{l}xt = 105000\\(80000 - x)(t + 1) = 225000\end{array} \right.$ qui conduit à ${x^2} + 250000x$ $- 8400000000 = 0$ et ses solutions sont 30 000 et -280 000.
La première part placée dans la deuxième banque est 30 000 FCFA.

N.B. : le barème réservé à la présentation porte sur l’ensemble de toute la copie du candidat.