Objectifs:
Étudier les phénomènes d’interférences et d’effet photoélectriques pour mettre en exergue le double aspect ondulatoire et corpusculaire de la lumière.
Introduction
Pour expliquer certains phénomènes tels que la diffraction, l’interférence lumineuse... on a dû admettre l’hypothèse des vibrations lumineuses; Cependant, cette hypothèse ne rend pas compte de l’absorption, de la production de la lumière. Elle se limite à sa propagation. Cette grave difficulté a conduit la physique moderne dans une voie de conciliation entre la vibration lumineuse et la structure granulaire de la lumière: l’effet photoélectrique.
I– Aspect ondulatoire de la lumière Cours sur la lumière
I– Aspect ondulatoire de la lumière
Nous avons montré que la lumière blanche qui traverse un prisme était décomposée en une infinité de couleur i.e. en une infinité de lumière monochromatique ( chacune caractérisée par sa propre longueur d’onde). L’ensemble de ces longueurs d’onde est appelé spectre visible de la lumière blanche compris entre : 0,40μm≤λ≤0,75μm
De part et d’autre du spectre visible, on a les ultraviolettes (UV) et les infrarouges (I R)
L’étude du phénomène d’interférence lumineux permet de mesurer chacune des longueurs d’onde.
I-1 Interférences lumineuses Cours sur la lumière
I-1 Interférences lumineuses
Plusieurs dispositifs tels que: les miroirs de Fresnel, les demi-lentilles de billet, les fentes d’Young... permettent d’étudier les phénomènes d’interférences
I.1.1 Obtention d’interférences lumineuses: les fentes d’Young Cours sur la lumière
I.1.1 Obtention d’interférences lumineuses: les fentes d’Young
Le dispositif expérimental est constitué d’une source de lumière monochromatique (S), d’une plaque (P) constituée de deux fentes parallèles et d’un écran (E) disposé parallèlement à la plaque.
On se propose :
— De déterminer l’expression de la différence de marche d2-d1
— D’évaluer l’influence du déplacement d’une source sur la différence de marche
— D’évaluer l’influence d’une lame à faces parallèles sur la différence de marche.
— De déterminer le lieu de la première coïncidence due à la superposition de deux systèmes de franges.
— De déterminer l’expression de l’intensité lumineuse.
* Expression de la différence de marche
La différence de marche est donnée par: δ=(SS2+S2M) −(SS1+S1M) =S2M−S1M =d2−d1 Car SS2=SS1
Dans le triangle S1AM : d21=D2+(x−a2)2
Dans le triangle S2BM : d21=D2+(x+a2)2, ainsi : d22−d21= D2+(x+a2)2 −(D2+(x−a2)2) =2ax ainsi : d22−d21= (d2−d1)(d2+d1) =2ax soit : δ=d2−d1 =2axd2+d1
En pratique, D≻≻a et D≻≻x, on peut alors faire l'approximation : d2+d1=2D. ainsi : δ=d2−d1=axD
Si le point M est sur une frange brillante, alors :δ=kλ avec k∈Z
Si M est sur une frange sombre,δ=(2k+1)λ2 avec k∈Z
Si δ=0le point M est sur la frange centrale.
* Expression de l’interfrange
L’inter-frange noté (i), est la distance entre les points homologues de deux franges consécutives de même nature.
Soient M1 et M2 deux points situés respectivement sur deux franges brillantes consécutives d’ordre k et k+1 : x1=kλDa et x2=(k+1)λDa soit i=x2−x1=λDa
* Influence du déplacement de la source sur la différence de marche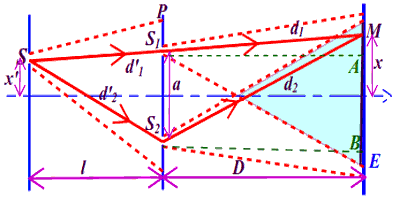 Dans ce cas, SS1est différent de SS2 , ainsi: δ=(SS2+S2M)− (SS1+S1M) =(SS2−SS1)+ (S2M−S1M)
Dans ce cas, SS1est différent de SS2 , ainsi: δ=(SS2+S2M)− (SS1+S1M) =(SS2−SS1)+ (S2M−S1M)
De la même façon, on montre qu’avec : l≻≻a et l≻≻x′, on a : d′2−d′1=2l donc δ=ax′l+axD
* Influence d’une lame à faces parallèles sur la différence de marche On montrera dans la partie exercice que : δ=axD−e(n−1)
On montrera dans la partie exercice que : δ=axD−e(n−1)
* Expression de l’intensité lumineuse
Young a montré que le vecteur lumineux en un point M recevant de la lumière de plusieurs sources
était la somme géométrique des vecteurs lumineux originaires des divers sources et que l’intensité lumineuse au point M était proportionnelle au carré de l’amplitude du vecteur résultant. soit : I(M)=kA2 avec A= 2acosπλ(d2−d2) K étant la constance de proportionnalité, d2−d1=xλi alors I(M)= 4a2kcos2(πλxλi) I(M)=2a2k(1+cos(2xπi))
On constate que l’intensité lumineuse dépend de la position du point M sur l’écran. * Superposition de deux systèmes de franges
* Superposition de deux systèmes de franges
En utilisant une lumière bleue et une lumière jaune par exemple de longueur d’onde respective λ1 et λ2. chaque lumière produit son propre système de franges. La frange centrale sera verte, de part et d’autre de la frange centre , il y a un décalage progressive des franges bleues et jaunes jusqu’à la nouvelle coïncidence ( nouvelle frange verte ).
Si N est le nombre d’inter-franges pour la lumière jaune à la première coïncidence, le nombre d’inter-franges pour la lumière bleue est N+1.
Si x est le lieu de la première coïncidence i.e. la distance entre deux franges bleues alors : x=N.i1 =(N+1).i2, Avec {i1=λ1Dai2=λ2Da, on a : N=λ2λ1−λ2
II– Aspect corpusculaire de la lumière Cours sur la lumière
II– Aspect corpusculaire de la lumière
Une laque de zinc polie et chargée négativement perd de sa charge si elle est exposée à la lumière UV: C’est l’effet photoélectrique
L’effet photoélectrique est l’extraction des électrons d’un métal lorsqu’il est convenablement éclairé par un rayonnement électromagnétique.
II.1 Expérimentation Cours sur la lumière
II.1 Expérimentation
Soit le schéma suivant constitué de:
- Une cellule photoélectrique;


- Un voltmètre
- Un galvanomètre
- Un générateur de tension variable
- Un interrupteur,
Une source de lumière polychromatique et un filtre qui ne laisse passer qu’une seule radiation caractérisée par la fréquence ϑ ( longueur d’onde λ ) Lorsque la cellule est éclairée, le galvanomètre indique le passage du courant: il y a donc émission des électrons par la cathode pour certaines radiations de fréquence supérieure à la fréquence seuil ϑs caractéristique du matériau qui constitue la cathode.
Lorsque la cellule est éclairée, le galvanomètre indique le passage du courant: il y a donc émission des électrons par la cathode pour certaines radiations de fréquence supérieure à la fréquence seuil ϑs caractéristique du matériau qui constitue la cathode.
La fréquence seuil est la fréquence minimale ϑs de la lumière incidente pouvant provoquer une émission photoélectrique.
II.2 Caractéristique photoélectrique Cours sur la lumière
II.2 Caractéristique photoélectrique
Lorsqu’on éclaire la cellule photoélectrique avec des radiations de fréquence ϑ≻ϑS, la puissance lumineuse P reçue par la cathode restant constante; on constate que la tension varie avec l’intensité de courant. La courbe I=f(U) obtenue est appelée caractéristique de la cellule photo-émissive.
L’intensité de saturation est : IS=n.eΔt
Avec n le nombre d’électrons émis par la cathode pendant l’intervalle de temps Δt.
Son allure est la suivante :  Si UAC≻0, les électrons émis par la cathode sont attirés par l’anode et son nombre croît avec la tension UAC avant de se stabiliser pour une certaine valeur de l’intensité de courant appelée intensité de saturation IS.
Si UAC≻0, les électrons émis par la cathode sont attirés par l’anode et son nombre croît avec la tension UAC avant de se stabiliser pour une certaine valeur de l’intensité de courant appelée intensité de saturation IS.
Si I≥IS alors, tous les électrons émis par la cathode sont captes par l’anode.
Si −U0≺UAC≺0,certains électrons émis par la cathode peuvent atteindre l’anode. Le champ électrique entre A et C crée une force sur l’électron dont l’effet tend à le ralentir. Plus la valeur absolu de UAC est grand dans l’intervalle défini plus haut, moins il y a d’électrons émis par C qui ont une vitesse suffisamment grande pour atteindre A.
Si UAC≥−U0 , l’intensité I est nulle et aucun électron émis par C ne parvient à A
II.3 Le potentiel d’arrêt Cours sur la lumière
II.3 Le potentiel d’arrêt
C’est le potentiel minimal permettant de donner aux électrons une énergie suffisante pour quitter le métal ( cathode )
Nous pouvons évaluer l’énergie transportée par les électrons lorsqu'ils quittent le métal; E=W(→F)= →F.→AC =|−e|.→E.→AC =eU0 E=eU0
Ainsi, lorsque la lumière (visible ou l'UV) rencontre une surface métallique, des électrons sont émis par cette surface avec une énergie cinétique indépendante de l'intensité de la lumière, mais qui augmente linéairement avec sa fréquence.
Einstein proposa comme explication: l'énergie d'un faisceau de lumière monochromatique arrive par paquets d'énergie hϑ (appelés "quantum d'énergie"). Si le quantum d'énergie hϑ est transmis à un électron, celui-ci sort du métal avec une énergie cinétique. EC=hϑ−W0 =hCλ−W0
où W0 est le travail d'extraction et h la constante de Planck.
1ère lois de Lenard:
L'émission photo électrique ne se produit que si la fréquence de radiation monochromatique tombant sur le métal est supérieure à la radiation limite caractéristique du métal considéré.ϑ>ϑS
Le travail d'extraction vaut : W0=hϑS =hCλS
C=3 108 m/s est la vitesse de la lumière dans le vide; h=6,62 10-34 J.sest la constance de Planck et λS, la longueur d’onde seuil.
Influence de la puissance P du rayonnement
2ème loi de Lenard:
L'intensité IS de saturation est proportionnelle à la puissance transportée par le faisceau lumineux reçu par la cathode.
Si on fait varier la puissance P du faisceau lumineux ( en déplaçant la source lumineuse ), on obtient la courbe ci-dessous, le potentiel d’arrêt n’étant pas modifié La vitesse maximale d’émission des électrons est donc indépendante de la puissance du rayonnement électromagnétique. Ce constat est en contradiction avec le comportement ondulatoire de la lumière : la théorie ondulatoire prévoit qu’une plus grande puissance du faisceau lumineux devrait augmenter la vitesse d’émission des électrons, donc augmenter le potentiel d’arrêt, ainsi: le nombre d’électrons émis par C par seconde est d’autant plus grande que la puissance P est grande
La vitesse maximale d’émission des électrons est donc indépendante de la puissance du rayonnement électromagnétique. Ce constat est en contradiction avec le comportement ondulatoire de la lumière : la théorie ondulatoire prévoit qu’une plus grande puissance du faisceau lumineux devrait augmenter la vitesse d’émission des électrons, donc augmenter le potentiel d’arrêt, ainsi: le nombre d’électrons émis par C par seconde est d’autant plus grande que la puissance P est grande
Influence de la fréquence ϑ du faisceau monochromatique
L'énergie cinétique maximum (Ec max) émis par la cathode est indépendante de la puissance du faisceau monochromatique incident. Elle ne dépend que la fréquence de la radiation monochromatique incidente et croît de façon affine avec cette fréquence. Ec,max=12mv2=eU0 Ec,max=h(ϑ−ϑS) =hC(1λ−1λS)
Relation d'Einstein (Prix Nobel 1921)
On constate qu’en augmentant la fréquence de la lumière incidente, le potentiel d’arrêt U0 augmente, ainsi, la vitesse maximale d’émission des électrons en C est de plus en plus grande. La courbe représentant l’évolution de U0 en fonction de la fréquence v est une droite croissante de pente h/e où h est la constante de Planck.
La courbe représentant l’évolution de U0 en fonction de la fréquence v est une droite croissante de pente h/e où h est la constante de Planck. U0=he(ϑ−ϑs)
U0=he(ϑ−ϑs)
La puissance d'une onde électromagnétique éclairant une surface est donnée par : P=NΔthϑ
N le nombre de photo reçu par la cathode.
II-4 Le rendement quantique d’une cellule photo électrique Cours sur la lumière
II-4 Le rendement quantique d’une cellule photo électrique
C’est le rapport n/N du nombre d’électrons émis par seconde sur le nombre de photon reçue par seconde par la cathode. Il es de l’ordre de 10-2 r=nN×100
On peut citer comme application de l’effet photoélectrique :
- L’automatisation des systèmes
- Les piles photovoltaïques
Conclusion
La lumière se comporte selon les conditions d’expérience comme une onde ou comme un corpuscule ( grain de lumière).

