Partie A : Évaluation des ressources

A. Évaluation des savoirs

Exercice I

1. Énoncer la propriété de Thalès.
2. Dans quelles conditions peut-on appliquer la propriété de Thalès dans un triangle ?
3. Énoncer de la réciproque de la propriété de Thales.
4. Quand dit-on que deux triangles sont semblables ?

Exercice II

Soient les phrases suivantes, compléter les espaces vides par les mots ou groupes de mots qui conviennent
• Si deux triangles sont semblables, alors leurs cotés sont deux à deux . .. . . . ..
• Si deux triangles . . . . . . ., alors leurs angles sont deux à deux de même mesure.
• Si deux triangles ont . . . . . . . deux à deux proportionnels, alors ils sont semblables.
• Si deux triangles ont . . . . . . deux à deux de même mesure, alors ils sont semblables.

Exercice III

Pour chaque ligne du tableau, une seule affirmation est vraie, Écris le numéro de la ligne suivi de la lettre de l’affirmation vraie.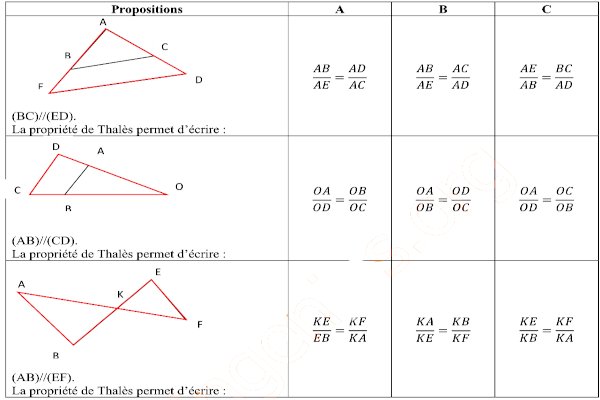

Exercice IV

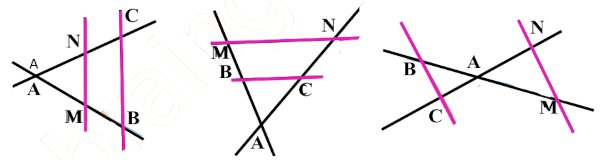
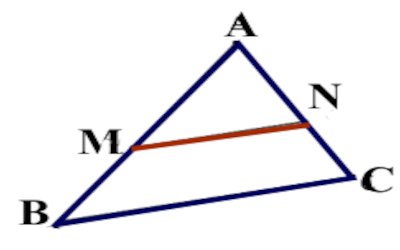Dans la figure ci-dessus, on a (\(\left( {BC} \right)\parallel \left( {MN} \right)\), Choisir la reponse exacte des propositions suivantes.
a) \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MB}}{{NC}}\) ;
b) \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\)
c) \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MB}}{{BN}}\)

B. Application des savoirs et des savoirs faire

Exercice I

Calculer \(x\) dans chacun des cas suivants.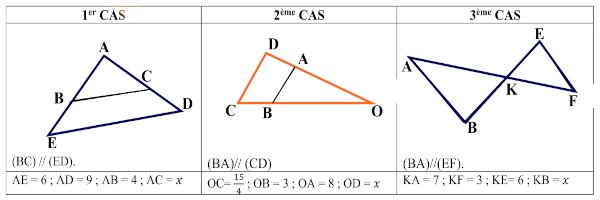

Exercice II

L’unité de longueur est le centimètre. ABC est un triangle tel que \(AB = 15\) ; \(AC = 5\).
Les points M et N appartiennent respectivement aux côtés [AC] et [AB] et sont tels que \(AM = 3\) ; \(AN = 9\).
Justifier que : \(\left( {MN} \right)\parallel \left( {CB} \right)\)

Exercice III

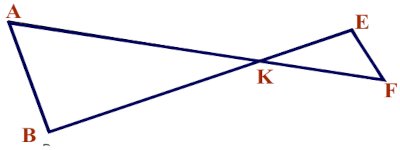On donne le triangle \(ABK\) ci-dessus. \(F \in \left[ {AK} \right]\) et \(E \in \left[ {BK} \right]\) tel que \(AK = 8\) ; \(KF = 3\) ; \(EF = 6\) et \(\left( {AB} \right)\parallel \left( {EF} \right)\).
Calcule \(AB\).

Partie B : Évaluation des compétences

Exercice I

Yéo a dans son jardin un anacardier et un manguier. Il se rappelle que lors de la visite de l’agent de l’agriculture, ce dernier avait déterminé les hauteurs de ces deux arbres mais il ne se rappelle que de la hauteur du manguier qui est 6,7 m. Son neveu qui est votre ami de classe vous sollicite afin de déterminer la hauteur de cet anacardier. Pour le faire, il se place à un endroit où ses yeux Y à 1,6 m du sol sont parfaitement alignés aves les cimes E et O des arbres. Les deux arbres sont distants de 30 mètres et la distance qui sépare le neveu de l’anacardier est de 20 mètres.
Sur la figure ci-dessous, les droites \((OW)\) et \((EA)\) sont perpendiculaires à \((YW)\).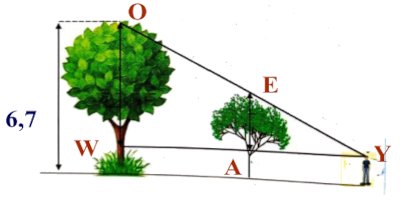
1) Justifie que les droites \((OW)\) et \((EA)\) sont parallèles.
2) Calcule la hauteur de l’anacardier.