Partie l- Évaluation des ressources / 24 points

Exercice 1 : Vérification des savoirs/ 8 points

1. Définir : grandeur sinusoïdale, potentiel d'arrêt d'une cellule photoémissive. 2 pt
2. Énoncer la loi de Coulomb. 2 pt
3. Donner le symbole normalisé d'un condensateur. 1 pt
4. Donner la condition pour obtenir le phénomène d'interférence à partir de deux sources ${O_1}$ et ${O_2}$. 2 pt
5- Répondre par Vrai ou Faux 1 pt
5-1 Deux grandeurs physiques de natures différentes peuvent avoir la même dimension.
5-2 L’énergie emmagasinée par un condensateur vérifie la relation $Q = CU$. .

Exercice 2 :Application des savoirs / 8 points

1. Phénomènes ondulatoires / 4 points

On admet qu'avec les fentes de YOUNG, la différence de marche entre les rayons ${S_1}M$ et ${S_2}M$ qui interférent en un point $M$ de l'écran $E$ est $\delta = \frac{{ax}}{D}$ que pour la frange brillante d’ordre $k$, $\delta = k\lambda$ (avec $k \in {\mathbb{Z}^*}$)
1.1 Exprimer $x$ en fonction de $k$, $\lambda$, $a$ et $D$ 1pt
1.2 Sachant que l’interfrange $i = {x_{k + 1}} - {x_k}$, Donner l’expression de $i$ en fonction de $a$, $D$ et $\lambda$, (longueur d'onde de la radiation lumineuse émise par la source S). 1 pt
1.3 Déterminer l’interfrange $i$ si la distance entre la frange centrale et la 9ème frange brillante est $d = 8$ mm. 2 pt

2. Circuit RLC /4 points

Entre deux points $P$ et $Q$, on maintient la différence de potentiel sinusoïdale est $u = 141,1\sin \omega t$ en volt.
2.1 La pulsation étant égale à $100\pi$rad/s, calculer la fréquence et la valeur efficace de cette tension. 2 pt
2.2 On place entre $P$ et $Q$ une bobine $(L, r)$ et un condensateur $C$, en série.
Déterminer l’impédance $Z$ du circuit. On donne: $L = 0,1 H$; $r = 2\Omega$; $C = 2 \times {10^{ - 6}}F$ 2 pt

Exercice 3 : Utilisation des savoirs/ 8 points

1. Radioactivité /4 points

Le polonium $210\left( {{}_{84}^{210}Po} \right)$ est un nucléide $\alpha$ , le noyau fils est un isotope du plomb $\left( {{}_{82}^{206}Pb} \right)$.
1.1 Écrire l’équation de désintégration d'un noyau de polonium 210. 2 pt
1.2 La demi-vie du polonium 210 est T = 138 jours.
1.2.1 Déterminer sa constante radioactive $\lambda$. 1pt
1.2.2 Un échantillon de polonium 210 a une activité ${A_0} = {10^{10}}$Bq à $t = 0$. Calculer le nombre ${N_0}$ de noyaux présents dans l’échantillon si $\lambda = 5,81 \times {10^{ - 8}}{s^{ - 1}}$ 1 pt

2. interférences mécaniques /4 points

On dispose d'un diapason entretenu électriquement dont les branches sont animées d'un mouvement sinusoïdal de fréquence 200 Hz et d'amplitude $a$. A une branche du diapason, on fixe une tige supportant deux pointes distantes de 1,4 cm et produisant en deux point ${S_1}$ et ${S_2}$ de la surface d’un liquide, deux perturbations en phase et de même amplitude. Les ondes se propagent à la surface du liquide avec une vitesse $V = 0,4m/s$.
2.1 Déterminer l'état vibratoire d'un point $M$ situé à 18 mm de ${S_1}$ et à 9 mm de ${S_2}$. 2 pt
2.2 Déterminer le nombre de ligne d'amplitude maximale entre ${S_1}$ et ${S_2}$. 2 pt

Partie II : Évaluation des compétences / 16 points

Situation problème
Au cours d’un concours scientifique, deux tâches sont proposées à chaque groupe de deux candidats. Lors du passage du groupe constitué de AKONO et BENJl, les tâches suivantes leur sont proposés : '
Tâche 1
Il leur est demandé d’identifier le satellite géostationnaire parmi les quatre ci-après.
Après un travail individuel, les deux sont en désaccord sur la réponse à donner.
Tâche 2 .
Il leur est demandé de déterminer la tension $U$ entre les plaques ${P_1}{P_2}$; qui permet de loger, les ions $B{r^ - }$ dans le trou $P$ après avoir été successivement accélérés entre $O$ et $A$ et subit une déviation sous l'effet du champ magnétique (voir figure ci-dessous)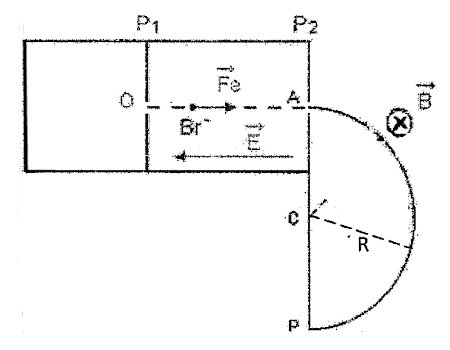
Les deux amis proposent les résultats différents. AKONG propose $U = 1,00 \times {10^3}V$ et le BENJI propose $U = 1,00 \times {10^2}V$.
Informations utiles :
Sur le satellite
• Orbite circulaire et vitesse constante.
• L'orbite géostationnaire est une orbite située à 35786 km d’altitude dans le plan équatorial.
• Expression de la vitesse du satellite : $V = {R_T}\sqrt {\frac{{{g_0}}}{{\left( {{R_T} + h} \right)}}}$
Données:
Rayon de la Terre ${R_T} = 6371km$
Intensité du champ gravitationnel sur la surface de la terre ${g_0} = 9,8m/{s^2}$.
Sur la déviation des ions
Les ions entrent dans la chambre d'accélération par le point 0 sans vitesse initiale.
Expression du rayon de courbure de la trajectoire des ions : $R = \frac{{m.V}}{{\left| q \right|.B}}$
Données: AP = 0,811 m; B = 0,1 T; $q = - 1,6 \times {10^{ - 19}}C$, $m = 1,31 \times {10^{ - 25}}kg$
En exploitant tes informations ci-dessus et à l'aide d'une démarche scientifique,
1. Départage AKONO et BENJI sur le satellite qui correspond. 8 pt
2. Aide les deux candidats à choisir le bon résultat. 8 pt