Partie l- Évaluation des ressources / 24 points

Exercice 1 : Vérification des savoirs/ 8 points

Définition : 2 pt
• Grandeur sinusoïdale : c'est une grandeur dont l'expression est une fonction sinusoïdale du temps.
• Potentiel d'arrêt d'une cellule photoémissive : valeur absolue de la tension qui annule le courant photoélectrique.
3. Énonçons la loi de Coulomb. 2 pt
La force d'attraction ou de répulsion qui s'exerce entre deux charges ponctuelles \({q_A}\) et \({q_B}\), placées respectivement aux points A et B est:
• dirigée suivant la droite (AB);
• proportionnelle à \({q_A}\) et \({q_B}\);
• inversement proportionnelle au carré de la distance qui sépare les deux charges.
\({\overrightarrow F _{A/B}} = - {\overrightarrow F _{B/A}} = \) \(k\frac{{{q_A}{q_B}}}{{A{B^2}}}\overrightarrow {{u_{AB}}} \)
3. Donnons le symbole normalisé d'un condensateur. 1 pt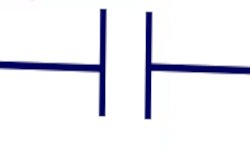
4. Donnons la condition pour obtenir le phénomène d'interférence à partir de deux sources \({O_1}\) et \({O_2}\). 2 pt
Les sources \({O_1}\) et \({O_2}\) doivent être cohére tn es et synchrones.
5- Répondre par Vrai ou Faux 1 pt
5-1 Faux
5-2 Faux

Exercice 2 :Application des savoirs / 8 points

1. Phénomènes ondulatoires / 4 points

1.1 Exprimons \(x\) en fonction de \(k\), \(\lambda \), \(a\) et \(D\) 1pt
\(k\lambda = \frac{{ax}}{D} \Rightarrow x = \frac{{k\lambda D}}{a}\)
1.2 Sachant que l’interfrange \(i = {x_{k + 1}} - {x_k}\), Donnons l’expression de \(i\) en fonction de \(a\), \(D\) et \(\lambda \), (longueur d'onde de la radiation lumineuse émise par la source S). 1 pt
\(i = {x_{k + 1}} - {x_k} = \left( {k + 1} \right)\) \(\frac{{\lambda D}}{a} - k\frac{{\lambda D}}{a} \Rightarrow \) \(i = \frac{{\lambda D}}{a}\)
1.3 Déterminons l’interfrange \(i\) si la distance entre la frange centrale et la 9ème frange brillante est \(d = 8\) mm. 2 pt
\(d = 9i \Rightarrow i = \frac{d}{9}\)
AN : \(i = 0,89mm\)

2. Circuit RLC /4 points

2.1 La pulsation étant égale à \(100\pi \)rad/s, calculons la fréquence et la valeur efficace de cette tension. 2 pt
\(\omega = 2\pi f \Rightarrow f = \frac{\omega }{{2\pi }}\)
AN : \(f = 50Hz\)
Valeur efficace de la tension:
\(U = \frac{{Um}}{{\sqrt 2 }}\)
AN : \(U = 99,8V\)
2.2 Déterminons l’impédance \(Z\) du circuit. On donne: \(L = 0,1 H\); \(r = 2\Omega \); \(C = 2 \times {10^{ - 6}}F\) 2 pt
\(Z = \sqrt {{r^2} + {{\left( {L\omega - \frac{1}{{C\omega }}} \right)}^2}} \)
AN : \(Z = 1,56 \times {10^3}\Omega \)

Exercice 3 : Utilisation des savoirs/ 8 points

1. Radioactivité /4 points

1.1 Écrivons l’équation de désintégration d'un noyau de polonium 210. 2 pt
\({}_{84}^{210}Po \to {}_{82}^{206}Pb + {}_2^4He\)
1.2 La demi-vie du polonium 210 est T = 138 jours.
1.2.1 Déterminons sa constante radioactive \(\lambda \). 1pt
\(\lambda = \frac{{\ln 2}}{T}\)
AN : \(\lambda = 5,81 \times {10^{ - 8}}{s^{ - 1}}\)
1.2.2 Calculons le nombre \({N_0}\) de noyaux présents dans l’échantillon si \(\lambda = 5,81 \times {10^{ - 8}}{s^{ - 1}}\) 1 pt
\({A_0} = \lambda {N_0} \Rightarrow {N_0} = \frac{{{A_0}}}{\lambda }\)
AN : \({N_0} = 1,72 \times {10^{17}}Bq\)

2. interférences mécaniques / 4 points

2.1 Déterminons l'état vibratoire d'un point \(M\) situé à 18 mm de \({S_1}\) et à 9 mm de \({S_2}\). 2 pt
\(\frac{{{d_2} - {d_1}}}{\lambda } = \frac{{\left( {{d_2} - {d_1}} \right)t}}{v}\)
AN : \(\frac{{{d_2} - {d_1}}}{\lambda } = - 4,5\)
On a la forme \(\frac{{{d_2} - {d_1}}}{\lambda } = k + \frac{1}{2}\) ; donc M est au repos.
2.2 Déterminons le nombre de ligne d'amplitude maximale entre \({S_1}\) et \({S_2}\). 2 pt
\( - {S_1}{S_2} \prec {d_2} - {d_1} \prec {S_1}{S_2}\)
Or \({d_2} - {d_1} = k\lambda = \frac{{kV}}{f}\),
on a \( - {S_1}{S_2} \prec \frac{{kV}}{t} \prec {S_1}{S_2} \Leftrightarrow \) \( - {S_1}{S_2}\frac{f}{V} \prec k \prec \frac{f}{V}{S_1}{S_2}\) alors \( - 7 \prec k \prec 7\)
Ainsi, entre \({S_1}\) et \({S_2}\), il y a 13 lignes d'ampliitude maximale.

Partie II : Évaluation des compétences / 16 points

. Il s'agit de déterminer la vitesse linéaire d'un satellite géostationnaire afin de se 5 prononcer.
Pour cela, nous allons:
(i) Utiliser l’expression de la vitesse d'un satellite (donnée) pour calculer la vitesse d'un satellite géostationnaire ;
(ii) Comparer la valeur obtenue aux valeurs du tableau et conclure.
Vitesse d’un satellite géostationnaire :
\(V = {R_T}\sqrt {\frac{{{g_0}}}{{{R_T} + h}}} \)
AN : \(V \approx 3072m.{s^{ - 1}}\)
Comparaison et conclusion
La valeur obtenue est égale à celle du satellite \({S_4}\). Ainsi c'est \({S_4}\) qui est un satellite géostationnaire.
2. Il s'agit de déterminer la tension électrique entre les plaques \({P_1}\) et \({P_2}\) afin d aider les deux candidats à choisir le bon résultat.
Pour cela, nous allons :
(i) Calculer le rayon de courbure \(R\) de la trajectoire circulaire.
(ii) Utiliser l'expression du rayon de L courbure donnée pour déterminer la vitesse au point A ;
(iii) Utiliser le théorème de l'énergie cinétique pour déduire la tension entre les plaques \({P_1}\) et \({P_2}\) ;
(iv) Comparer la valeur obtenue aux valeurs des deux candidats et conclure.
Rayon de courbure
\(R = \frac{{AP}}{2}\)
AN : \(R = 0,4055m\)
Vitesse du point A : \(R = \frac{{mV}}{{\left| q \right|B}} \Rightarrow V = \frac{{R\left| q \right|B}}{m}\)
AN : \(V = 49526,7\) m/s
Tension entre les plaques \({P_1}\) et \({P_2}\)
Le TEC appliqué à l’ion entre les points O et A:
\({E_{{C_A}}} - {E_{{C_0}}} = W(\overrightarrow F ) \Leftrightarrow \) \(\frac{1}{2}m{V^2} - 0 = \left| q \right|U\)
Soit \(U = \frac{1}{{2\left| q \right|}}m{V^2}\)
AN : \(U = 1,004 \times {10^{ - 3}}V\)
Comparaison et conclusion
\(U = 1,004 \times {10^{ - 3}}V\) , donc le bon résultat est celui du candidat AKONO.