Cette épreuve étalée sur deux pages, est constituée de deux parties Indépendantes

Partie A : Évaluation des ressources ( 15 points)

L'unité de longueur est le centimètre.
ABC est un triangle rectangle en A et de sens direct avec AB = 4.
I est le milieu du côté [BC] et G, le barycentre des points A ,B et C affectés respectivement des coefficients 2, 1 et 1
1) Démontrer que G est le milieu de [AI] 1 pt
2) Soit \(\left( \Sigma \right)\) le lieu des points M du plan tas que \(\left\| {2\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right\| = BC\)
Démontrer que \(\left( \Sigma \right)\) est un cercle de centre G et passent par A.
Faire une figure où on représentera \(\left( \Sigma \right)\). 2 pt
3) Déterminer et représenter l’image \(\left( \Sigma ‘ \right)\) de \(\left( \Sigma \right)\) par la rotation \(r\) de centre A et d’angle de mesure \( - \frac{\pi }{2}\) 1 pt

Exercice II : (5points)

On considère tes fonctions numériques \(f\) et \(g\) à variable réelle définie par les expressions \(f(x) = - {x^3} + 3{x^2}\) et \(g(x) = a{x^3} + b{x^2} + cx + 4\) où a, b et c sont des réels donnés.
Le plan est rapporte au repère orthonormé \(\left( {O;\overrightarrow i ,\overrightarrow j } \right)\). \((Cf)\) est la courbe de \(f \)et \((Cg)\), celle de \(g\).
1) Résoudre dans \(\mathbb{R}\), le système d’inconnue (X,,Y,Z) suivant :
\(\left\{ \begin{array}{l}27X + 9Y + 3Z = 0\\X + Y + Z = - 4\\27X + 6Y + Z = 0\end{array} \right.\)
2) Déterminer les réels a, b et c sachant que \((Cg)\) coupe l’axe des abscisses au point d’abscisse 1 et admet au pointe S de coordonnées (3, 4) une tangente parallèle à faxe des abscisses.(1 pt)
3) Dresser le tableau de variation de \(f\) et tracer avec soin le courbe \((Cf)\). (2 pts)
4) Vérifier que \(g(x) = f(x - 1)\). Représenter alors la courbe \((Cg)\). (1 pt)

Exercice 3 ( 3 points)

1) Démontrer que pour tout réel \(x\) , on a \( - 2 + \cos x \prec 0\) (0,25,pt)
2) Démontrer que pour tout réel \(x\) , on a \( - 3\cos x - 2{\sin ^2}x = \) \((1 + 2\cos x)( - 2 + \cos x)\). (0,5 pt)
3) Résoudre alors dans \(\left[ {0,2\pi } \right[\), l’equation \( - 3\cos x - 2{\sin ^2}x = 0\) (1,5 pt)
4) Résoudre dans \(\left[ {0,2\pi } \right[\), l’inéquation \( - 3\cos x - 2{\sin ^2}x \succ 0\) . (0,75 pt)

Exercice 4 : (3 points)

À la question «quels temps consacrez-vous à la télévision le dimanche? ››, des individus d'une population ont fourni des réponses résumées dans le tableau statistique suivant :
1) Déterminer le temps moyen consacré à la télévision le dimanche. (0,5 pt)
2) Construire la courbe des fréquences cumulées croissantes encore appelé polygone des fréquences cumulées croissantes. (1,5 pt)
3) Déterminer la médiane de cette série statistique. (1 pt)

PARTIE B : Évaluation des compétences (5 points)

Situation :
Kassim a emprunté (sans intérêt) dans une banque de PME, une somme de 20 millions de francs CFA pour un projet d'élevage des chèvres sur une partie de son vaste domaine traversée par une rivière rectiligne.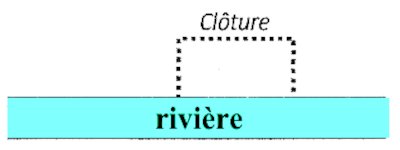
Il doit rembourser cet emprunt en déposant chaque année le même montant dans cette banque. Elle se souvient que le banquier lui avait dit que si elle déposait chaque année 0,5 million de francs CFA de plus, alors sa dette serait épongée 2 ans plus tôt.
La 1ere partie du projet consiste à délimiter par une clôture et une bordure de la rivière, une surface rectangulaire d'aire 4,5 ha, comme indique la figure ci-dessus où le côté ouvert a l’eau n'a pas besoin de clôture. Les dimensions de cet espace doivent être choisies de telle sorte que la clôture (en pointillés) soit la moins longue possible.
La 2nde partie du projet consiste à creuser la fondation de la clôture et à faire les constructions par la suite. Le technicien en charge des travaux a promis de creuser la fondation sur une longueur de 20,5 m le 18' jour et, pour les autres jours.de travail, d'ajouter 1 m sur le nombre de mètres de fondation creusée la veille. Il au aussi promis de garder ce rythme au moins sur une longueur de 600 m de clôture.

Tâches
1) Déterminer le montant de chaque dépôt d'argent dont Kassim a besoin pour éponger sa dette et le nombre de ces dépôts. (1,5 pt)
2) Comment choisir les dimensions de l’espace rectangulaire à délimiter pour que la longueur totale de la clôture soit minimale ? (1,5 pt)
3) Combien de jours faudra-t-il au technicien pour creuser la fondation sur une longueur de 600 m ? (1,5 pt)
Présentation (0,5 pt)