PARTIE A : Évaluation des Ressources (15 points)

Exercice 1 4 points

1. Démontrons que G est le milieu de [AI]. 1 pt
I est le milieu de [BC], c'est-à-dire 1 = bar{(B;1),(C; 1)}. G = bar{(A; 2), (B; 1), (C; 1)}; ainsi G = bar{(A; 2), (1; 2)} donc G est le milieu de [AI].
2. Démontrons que $\left( \Sigma \right)$ est un cercle de centre G passant par A et faisons une figure où on représentera $\left( \Sigma \right)$. 2 pt
• $\left\| {2\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right\| = BC$ $\Rightarrow \left\| {4\overrightarrow {MG} } \right\| = BC$ puisque G = bar{(A; 2), (B;1), (C; 1)}.
Ainsi $MG = \frac{{BC}}{4}$-. Donc $\left( \Sigma \right)$ est le cercle de centre G et de rayon $\frac{{BC}}{4}$.
$\left\| {2\overrightarrow {AA} + \overrightarrow {AB} + \overrightarrow {AC} } \right\|$ $= \left\| {\overrightarrow {AB} + \overrightarrow {AC} } \right\|$
${\left\| {\overrightarrow {AB} + \overrightarrow {AC} } \right\|^2} = {(\overrightarrow {AB} )^2}$ $+ {(\overrightarrow {AC} )^2} + 2\overrightarrow {AB} .\overrightarrow {AC}$
${(\overrightarrow {AB} )^2} + {(\overrightarrow {AC} )^2} = B{C^2}$ car ABC est triangle rectangle en A. Ainsi $\left\| {2\overrightarrow {AA} + \overrightarrow {AB} + \overrightarrow {AC} } \right\| = BC$; donc $A \in \left( \Sigma \right)$.
$\left( \Sigma \right)$ est donc le cercle de centre G passant par A.
Faisons la figure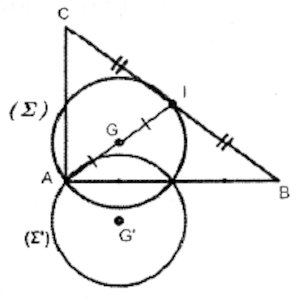
3) Déterminons et représentons $\left( {\Sigma '} \right)$ image de $\left( \Sigma \right)$ par la rotation $r$ de centre A et d'angle $- \frac{\pi }{2}$. 1 pt
$\left( {\Sigma '} \right)$ est le cercle de centre G' image de G par la rotation $r$ et de même rayon que $\left( \Sigma \right)$
Pour la représentation de $\left( {\Sigma '} \right)$, voir figure précédente.

EXERCICE 2 ; (5 points)

1. Résolvons dans ${\mathbb{R}^3}$ le système d'inconnue $(X; Y; Z)$.
$\left\{ \begin{array}{l}27X + 9Y + 3Z = 0\\X + Y + Z = - 4\\27X + 6Y + Z = 0\end{array} \right.$ 1 pt
$27X + 6Y + Y = 0$ $\Rightarrow Z = - 27X - 6Y$. En substituant Z dans les deux autres équations du système on obtient $\left\{ \begin{array}{l}6X + Y = 0\\ - 26X - 5Y = - 4\end{array} \right.$
Soit $\left\{ \begin{array}{l}X = - 1\\Y = 6\\Z = - 9\end{array} \right.$
2. Déterminons les réel a, b et c sachant que (Cg) coupe l'axe des abscisses au point d'abscisse 1 et admet au point S de coordonnées (3; 4) une tangente parallèle à l'axe des abscisses. 1 pt
$g(x) = a{x^3} + b{x^2} + cx + 4$
• $g(1) = 0 \Rightarrow$ $a + b + c + 4 = 0$
• $g(3) = 4 \Rightarrow$ $27a + 9b + 3c = 0$
• $g'(3) = 0 \Rightarrow$ $27a + 6b + c = 0$
D’après le système précèdent $a = -1$, $b = 6$ et $c = - 9$
3.) Dressons le tableau de variation de f et traçons avec soin la courbe $\left( {Cf} \right)$ 2 pts
$f(x) = - {x^3} + 3{x^2}$
• $Df = \mathbb{R}$
• $\mathop {\lim }\limits_{x \to - \infty } f(x) = + \infty$ et $\mathop {\lim }\limits_{x \to + \infty } f(x) = - \infty$
• $f$ est dérivable sur $\mathbb{R}$ et pour tout réel $x$, $f'(x) = - 3{x^2} + 6x$
• $f'(x) = 0$ équivaut à $x=0$ ou $x=2$.
• Tableau de variation :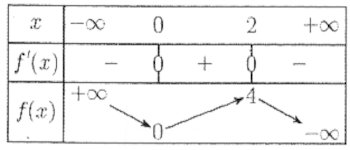
• Courbe représentative
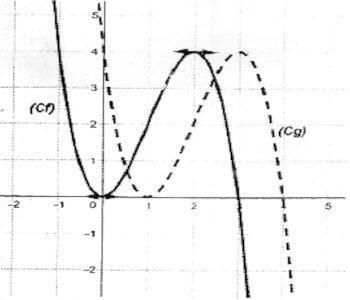4) Vérifions que $g(x) = f(x - 1)$ et représentons alors la courbe $(Cg)$.
Soit $x$ un réel, $g(x) = - {x^3} + 6{x^2} - 9x + 4$
$f(x - 1) = - {x^3} + 6{x^2}$ $- 9x + 4 = g(x)$
Donc $g(x) = f(x - 1)$
• Représentons graphiquement la courbe $(Cg)$, $(Cg)$ est limage de $(Cf)$ par la translation de vecteur $\overrightarrow i$ ( voir figure)

Exercice 3 ( 3 points)

1. Démontrons que pour tout $x$, on a $- 2 + \cos x \prec 0$ 0, 75 pt
Pour tout $x$, $- 1 \le \cos x \le 1$ ainsi $- 3 \le - 2 + \cos x \le - 1 \prec 0$
Donc pour tout $x$, $- 2 + \cos x \prec 0$
2) Démontrons que pour tout $x$, on a $- 3\cos - 2{\sin ^2}x =$ $\left( {1 + 2\cos x} \right)\left( { - 2 + \cos x} \right)$
Soit $x$ un nombre réel
$- 3\cos - 2{\sin ^2}x =$ $- 3\cos x - 2\left( {1 - {{\cos }^2}x} \right) =$ $2{\cos ^2} - 3\cos x - 2 =$ $\left( {1 + 2\cos x} \right)\left( { - 2 + \cos x} \right)$
Donc pour tout réel $x$, $- 3\cos x - 2{\sin ^2}x =$ $\left( {1 + 2\cos x} \right)\left( { - 2 + \cos x} \right)$ 0,5 pt
3) Résolvons alors dans $\left[ {0,2\pi } \right[$, l’équation $- 3\cos - 2{\sin ^2}x = 0$
$- 3\cos - 2{\sin ^2}x = 0 \Leftrightarrow$ $\left( {1 + 2\cos x} \right)\left( { - 2 + \cos x} \right) = 0$
Soit $\left( {1 + 2\cos x} \right) = 0$ ou $\left( { - 2 + \cos x} \right) = 0$
Ainsi $\left( {1 + 2\cos x} \right) = 0$ $\cos x = - \frac{1}{2}$
Dans $\mathbb{R}$, $x = \frac{{2\pi }}{3} + 2k\pi$ et $x = - \frac{{2\pi }}{3} + 2$ avec $k \in \mathbb{Z}$
Dans $\left[ {0,2\pi } \right[$,$x = \frac{{2\pi }}{3}$ ou $x = \frac{{4\pi }}{3}$
4) Résolvons dans $\left[ {0,2\pi } \right[$, l’inéquation $- 3\cos x - 2{\sin ^2}x \succ 0$
A partir du tableau de signe de $- 3\cos x - 2{\sin ^2}x$, vous trouverez ${S_{\left[ {0,2\pi } \right[}} = \left] {\frac{{2\pi }}{3},\frac{{4\pi }}{3}} \right[$

Exercice 4 / ( 3 points )

1) Déterminons le temps moyen consacré à la télévision le dimanche 0,5 pt
$M = \frac{{357,5}}{{100}} = 3,575$
2.) Construisons la courbe des fréquences cumulées croissantes. 1,5 pt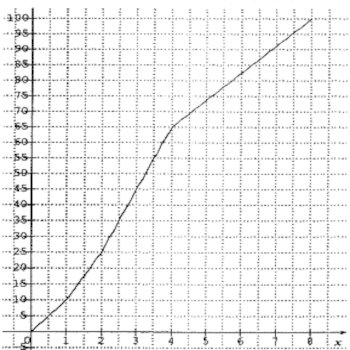
3) Déterminons la médiane de cette série statistique. 1 pt
Désignons par ${{m_e}}$cette médiane.
Par interpolation linéaire ou par lecture graphique, on a : $\frac{{{m_e} - 3}}{{50 - 45}} = \frac{{4 - 3}}{{65 - 45}}$
Donc ${m_e} = 3,25$

PARTIE B: Évaluation des compétences (5 points)

1) Déterminons le montant de chaque dépôt d'argent dont KASSIM a besoin pour éponger sa dette et le nombre de ces dépôts.
Désignons par $n$ le nombre de dépôts.
• Le montant de chaque dépôt est : $\frac{{20000000}}{n}$
Le montant de chaque dépôt si la dette était épongée 2 ans plutôt est : $\frac{{20000000}}{{n - 2}}$
$\frac{{20000000}}{{n - 2}} =$ $\frac{{20000000}}{n} + 500000$; soit $\frac{{200}}{{n - 2}} = \frac{{200}}{n} + 5$
On obtient $5{n^2} - 10n - 400 = 0$; son ${n^2} - 2n - 80 = 0$
$\left\{ \begin{array}{l}n = - 8\\n = 10\end{array} \right.$
Or $n$ est un entier positif donc $n = 10$
Le montant de chaque dépôt est $\frac{{20000000}}{{10}} = 2000000$
Donc Kassim effectuera 10 dépôts et le montant de chaque dépôt est de 2 000 000 FCFA
2) Trouvons comment choisir les dimensions de l'espace rectangulaire à délimiter pour que la longueur totale de la clôture soit minimale.
Désignons respectivement par $x$ et $y$ la largeur et la longueur en mètres de cet espace rectangulaire. $x \succ 0$ et $y \succ 0$.
Longueur de la clôture $L = 2x + y$.
On a $xy = 4,5ha$ = 45 000 m2 donc $y = \frac{{45000}}{x}$
Ainsi $L = 2x + \frac{{45000}}{x} =$ $\frac{{2{x^2} + 4500}}{x}$
Soit $L$ la fonction qui à $x$ associe $L = \frac{{2{x^2} + 4500}}{x}$
$L'(x) = 2 - \frac{{45000}}{{{x^2}}}$ $= \frac{{2{x^2} - 45000}}{{{x^2}}}$, $L'(x) = 0$ équivaut à $x = 150$ car $x \succ 0$.
A partir du tableau de variation, pour que la longueur totale de la clôture soit minimale (600m), la largeur doit être égale à 150m et la longueur égale à $y = \frac{{45000}}{{150}} = 300$; soit $300$ m
3) Déterminons le nombre de jours qu'il faudra au technicien pour creuser la fondation sur une longueur de 600 m..
Désignons par ${u_n}$ le nombre de mètres creusés; par le technicien le jour de rang $n$ ;
On a ${u_1} = 20,5$ et ${u_{n + 1}} = {u_n} + 1$. $\left( {{u_n}} \right)$ est une suite arithmétique de raison 1 et de premier terme ${u_1} = 20,5$; donc ${u_n} = \left( {n - 1} \right) + 20,5$
Désignons par ${S_n}$ la longueur totale creusée parle technicien au bout de $n$ jours de travail.
On a ${S_n} = {u_1} + {u_2} + ... + {u_n}$ $= \frac{{({u_1} + {u_n})n}}{2}$ $= \frac{{(40 + n)n}}{2}$
${S_n} = 600$ équivaut à $\frac{{(40 + n)n}}{2} = 600$ soit ${n^2} + 40n - 1200 = 0$
$\left\{ \begin{array}{l}n = 20\\n = - 60\end{array} \right.$
5 Donc il faudra 20 jours au technicien pour creuser les 600 m.

Présentation 0,5 pt