Partie A : Évaluation des ressources (13 points)

Exercice 1 : 4 points

Lors des oraux d'un concours, un candidat doit tirer au hasard successivement et sans remise trois questions dans une urne opaque qui contient 3 questions d'anglais, 4 questions de français et 5 questions de culture générale.
1) a) Déterminons le nombre de tirages possibles que le candidat peut effectuer. 1 pt
$A_{12}^3 = 1320$
b) Déterminons le nombre de tirages possibles comportant des questions de la même discipline. 1 pt
$A_3^3 + A_4^3 + A_5^3 = 90$
2) Réponse : b) 19, 96.
3) Réponse: d) 2.049

Exercice 2 : 3,5 points

On considère le polynôme $\mathbb{Q}$ à variable réelle $x$ défini par $Q(x) = - 2{x^2} - 9x + 5$
1) Résolvons dans $\mathbb{R}$ L’équation $Q(x) = 0$. 1,5 pt
$Q(x) = 0 \Leftrightarrow$ $- 2{x^2} - 9x + 5 = 0$
$\Delta = 121 \Rightarrow \left\{ \begin{array}{l}x = \frac{1}{2}\\x = - 5\end{array} \right.$
2) Étudions le signe du polynôme $Q(.-x)$. 1 pt
Tableau de signe :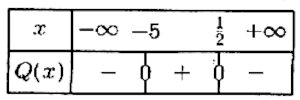

Donc $Q(x) \prec 0$, pour tout $x \in \left] { - \infty , - 5} \right[ \cup \left] {\frac{1}{2}, + \infty } \right[$
Et $Q(x) \succ 0$$x \in \left] { - 5,\frac{1}{2}} \right[$

Exercice 3 : 5,5 points

On considère la fonction numérique $f$ de la variable réelle $x$ définie dans
$\left[ { - 6; - 2} \right[ \cup \left] { - 2;4} \right]$ par $f(x) = \frac{{x - 1}}{{x + 2}}$ $(C)$ est la courbe représentative de $f$ dans un repère orthonormé $\left( {O;\overrightarrow i ,\overrightarrow j } \right)$
1) Calculons $\mathop {\lim }\limits_{x \to - {2^ - }} f(x)$ et $\mathop {\lim }\limits_{x \to - {2^ + }} f(x)$ 1 pt
$\mathop {\lim }\limits_{x \to - {2^ - }} f(x) = + \infty$ et $\mathop {\lim }\limits_{x \to - {2^ + }} f(x) = - \infty$
2) Déduisons une équation cartésienne de l’asymptote verticale à la courbe $(C)$. 0,5 pt
De ce qui précède, $x = - 2$ est asymptote verticale.
3. Montrons que pour tout réel $x$ distinct de -2, $f'(x) = \frac{3}{{{{\left( {x + 2} \right)}^2}}}$ 1 pt
$f'(x) =$ $\frac{{1\left( {x + 2} \right) - 1\left( {x - 1} \right)}}{{{{\left( {x + 2} \right)}^2}}}$ $= \frac{3}{{{{\left( {x + 2} \right)}^2}}}$ pour appartenant au domaine de définition.
4) Dressons le tableau de variations de $f$. 0,75 pt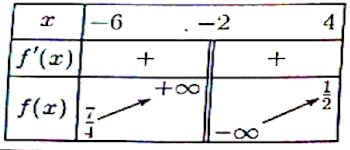
5) Écrivons une équation cartésienne de la tangente $(T)$ à $(C)$ au point d'abscisse 0. 0,75 pt
$(T):y = f'(0)(x - 0) +$ $f(0) = \frac{3}{4}x - \frac{1}{2}$
6) Traçons dans le repère $\left( {O;\overrightarrow i ,\overrightarrow j } \right)$ la droite $(T)$, la courbe $(C)$ et son asymptote. 1,5 pt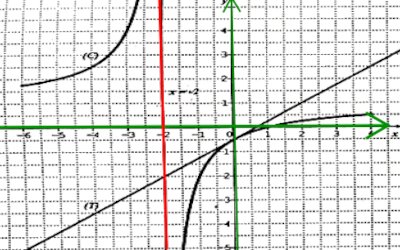

Partie B : Évaluation des compétences (7 points)

Tâche 1
Déterminons le montant déboursé par M.POKA pour l’achat du grillage utilisé pour son terrain
Désignons par $x$ et $y$ respectivement la longueur et la largeur de ce terrain.
$P = xy$ et $S = 2x + 2y$ soit le système : $\left\{ \begin{array}{l}x + y = 26\\xy = 168\end{array} \right.$ qui nous permet d’avoir l’équation ${x^2} - 26x + 168$ de solution $\Delta = 4 \Rightarrow \left\{ \begin{array}{l}x = 14\\y = 12\end{array} \right.$
La longueur du grillage est 14 rn.
Montant déboursé par M. POKA : $5000 \times 14 = 7000$ FCFA

Tâche 2 :
Calculons le montant que devrait débourser M.POKA pour l’achat de gateau apres la premiere hausse.
Désignons par $x$ la taux de chaque hausse ; $x \succ 0$
• Prix du gâteau après la première hausse : $20000 + \frac{{20000x}}{{10}}$ $= 20000 + 200x$
• Prix du gâteau après la deuxième hausse :
$20000 + \frac{{20000x}}{{10}} +$ $\frac{{\left( {20000 + 200x} \right)x}}{{100}} =$ $20000 + 400x + 2{x^2}$
Ainsi $20000 + 400x +$ $2{x^2} = 22050$ soit ${x^2} + 200x - 1025 = 0$
$\Delta = 44100 \Rightarrow x = 5$
La montant du gâteau après la première hausse ost : $20000 + 200 \times 5 = 21000$ FCFA.

Tâche 3

Déterminons le montant deboursee par M.POKA pour la participation de ses élèves aux olympiades.
Désignons par $n$ le nombre d'élèves. En supposant que la probabilité de participation de chacun des élèves est la même.
• Montant que chaque élève est supposé apporter avant le départ : $\frac{{96000}}{n}$ ;
• Montant que chaque élève est supposé apporter avant le départ et apres le désistement : $\frac{{96000}}{n}$ ; $\frac{{96000}}{{n - 2}}$
Ainsi $\frac{{96000}}{{n - 2}} = 4000 + \frac{{96000}}{n}$ $\Rightarrow {n^2} - 2n - 48 = 0$
$\Delta = 196 \Rightarrow x = 5\left\{ \begin{array}{l}n = - 6\\n = 8\end{array} \right.$
Donc la montant déboursé par M. POKA pour la participation de ses élèves est : $8000 \times 8 = 64000$ F CFA.